Difference Between Bubble Sort and Selection Sort

Bubble Sort repeatedly swaps adjacent elements until the list is sorted, while Selection Sort repeatedly selects the smallest (or largest) element and places it in its correct position. Both have O(n²) time complexity, but they differ in the number of swaps, comparisons, and efficiency in practice.

What is Bubble Sort?

The bubble sort is also one of the sorting techniques used for sorting the elements of an array. The basic principle behind the bubble sort is that the two adjacent elements are to be compared; if those elements are in correct order, then we move to the next iteration. Otherwise, we swap those two elements.

To read more Bubble Sort Algorithm

Example: Bubble Sort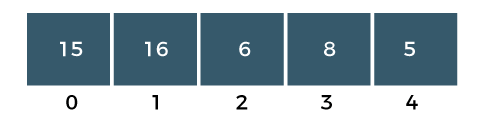

The above array is an unsorted array consists of 5 integers, i.e., 15, 16, 6, 8, 5.

Steps to Sort the Array

PASS 1

Step 1: The a[0] element is compared with a a[1] element. The a[0] is less than a[1], i.e., 15<16, so no swapping would be done as shown in the below figure: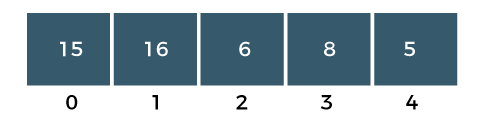

Step 2: Now, a[1] would be compared with a a[2] element. Since a[1] is greater than the a[0] element, i.e., 16>6, so swap 16 and 6 as shown in the below figure: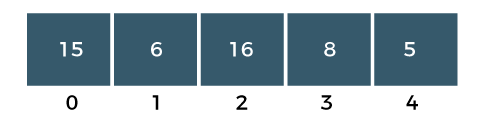

Step 3: The a[2] would be compared with a a[3] element. Since a[2] is greater than the a[3] element, i.e., 16>8, so swap 16 and 8 elements as shown in the below figure: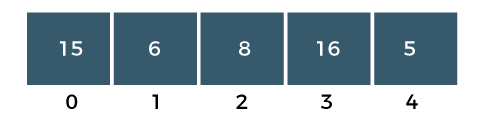

Step 4: The a[3] would be compared with a[4] element. Since a[3] is greater than the a[4], i.e., 16 > 5, so swap 16 and 5 elements as shown in the below figure:

As we can observe in the above array that the element which is the largest has been bubbled up to its correct position. In other words, we can say that the largest element has been placed at the last position of the array. The above steps are included in PASS 1in which the largest element is at its correct position.

We will again start comparing the elements from the first position in PASS 2.

PASS 2:

Step 1: First, we compare a[0] with a[1] element. Since a[0] element is greater than the a[1] element, i.e., 15 > 6, swap a[0] element with a[1] as shown in the below figure:

Step 2: The a[1] element would be compared with a[2] element. The a[1] is greater than the a[2], i.e., 15 > 8, so swap a[1] with element a[2] as shown in the below figure:

Step 3: The a[2] element would be compared with a a[3] element. Since a[2] is greater than the a[3] element, i.e., 15 > 5, swap element 15 with element 5 as shown in the below figure:

Step 4: Now, a[3] is compared to a[4]. Since a[3] is less than a[4], so no swapping would be done as shown in the below figure: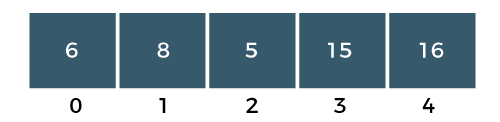

As we can observe above that the two elements are at the right position, largest (16) and the second largest element (15). In an array, three elements are unsorted, so again we will follow the same steps in PASS 3.

PASS 3:

Step 1: First, we compare a[0] with a[1]. Since a[0] is less than a[1], i.e., 6 < 8, so no swapping would be done as shown in the below figure: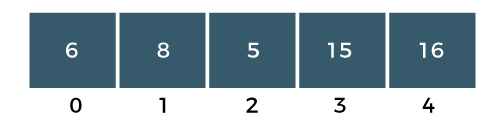

Step 2: Now, a[1] would be compared with a[2]. As a[1] is greater than a[2], so swap the element 8 with the element 5 as shown in the below figure: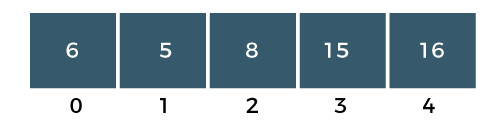

Step 3: The a[2] would be compared with a[3]. Since a[2] is less than a[3], i.e., 8 < 15, so no swapping would be done as shown in the below figure: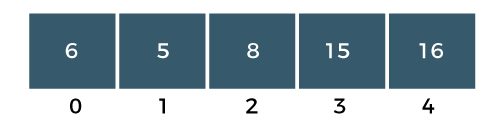

Step 4: The a[3] element would be compared with a[4]. Since a[3] is less than a[4], i.e., 15 < 16, so no swapping would be done as shown in the below figure: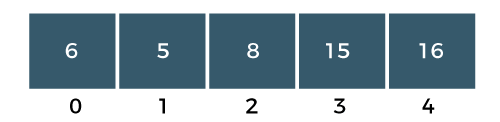

In PASS 3, three elements are at the right positions, largest, second largest and third largest. In an array, two elements are not sorted, so again we will follow the same steps in PASS 4.

PASS 4:

Step 1: First, we will compare a[0] and a[1]. Swap the a[0] with a[1] as a[0] is greater than a[1].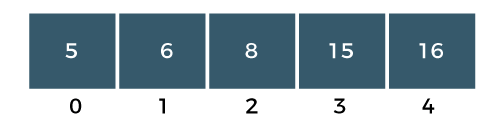

The above array is a sorted array as all the elements are at the correct positions.

Advantages of Bubble Sort

• Very easy to understand and implement.
• Best-case time complexity is O(n) (already sorted list).
• Stable sorting algorithm.
• Works well for small input sizes.
• Useful for educational demonstration of sorting concepts.

Disadvantages of Bubble Sort

• Highly inefficient for large datasets.
• Worst-case time complexity is O(n²).
• Performs too many unnecessary swaps.
• Not suitable for performance-critical systems.

What is Selection Sort?

Sorting means arranging the elements of an array in ascending order. Selection sort is one sorting technique used for sorting the array. In selection sort, an array is divided into two sub- arrays, i.e., one is an unsorted sub-array, and the other is sorted sub-array. Initially, we assume that the sorted subarray is empty. First, we will find the minimum element from the unsorted subarray, and we will swap the minimum element with an element which is at the beginning position of the array. This algorithm is named as selection sort because it is selecting the minimum element and then performs swapping.

To read more Selection Sort Algorithm

Example: Selection Sort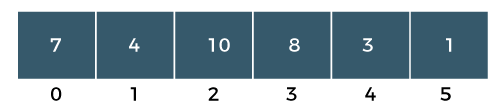

The above unsorted array contains 6 elements indexed starts from 0 and ends at 5.

Steps to Sort the Array

Step 1: In the above array, the minimum element is 1; swap element 1 with an element 7.

Now, the sorted array contains only one element, i.e., 1, while the unsorted array contains 5 elements, i.e., 4, 10, 8, 3, 7.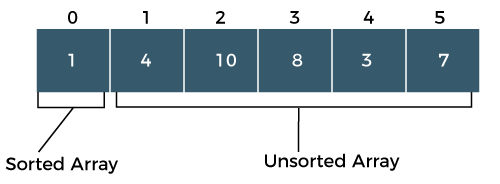

Step 2: In the unsorted sub-array, the minimum element is 3, so swap element 3 with an element 4, which is at the beginning of the unsorted sub-array.

Now the sorted array contains two elements, i.e., 1 and 3, while the unsorted array has four elements, i.e., 10, 8, 4, 7, as shown in the above figure.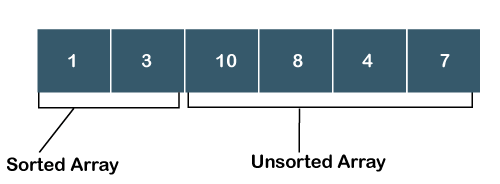

Step 3: Search the minimum element in the unsorted sub-array, and the minimum element is 4. Swap the element 4 with an element 10, which is at the beginning of the unsorted sub- array.

Now, the sorted array contains three elements, i.e., 1, 3, 4, while the unsorted array has three elements, i.e., 10, 8, 7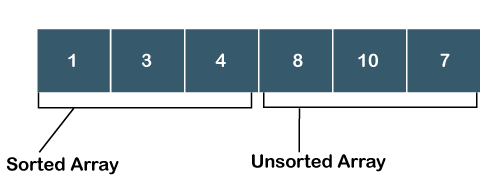

Step 4: Search the minimum element in the unsorted array, and the minimum element is 7. Swap element 7 with an element 10, which is at the beginning of the unsorted sub-array.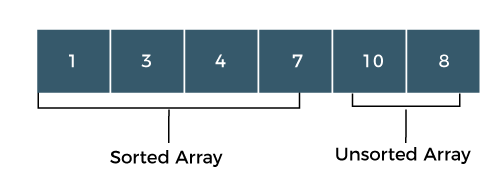

Now, the sorted array contains four elements, i.e., 1, 3, 4, 7, while the unsorted array has two elements, i.e., 10, 8.

Step 5: Search the minimum element in the unsorted array and the minimum element is 8. Swap the element 8 with an element 10 which is at the beginning of the unsorted sub-array.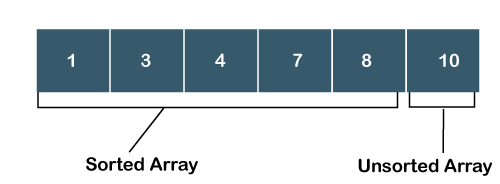

Now, the sorted array contains the elements, i.e., 1, 3, 4, 7, 8.

Step 6: The last element is left in the unsorted sub-array. Move the last element to the sorted sub array shown as below:

Advantages of Selection Sort

• Very simple sorting technique.
• Performs minimum number of swaps (only n swaps).
• Works well when swap operation is expensive.
• Easy to implement.
• Requires very little additional memory (in-place sorting).

Disadvantages of Selection Sort

• Time complexity is always O(n²), even in best case.
• Not stable; equal elements may lose original order.
• Inefficient for large datasets.
• Comparisons are high even when array is already sorted.
• Not suitable for real-time systems needing fast results.

Differences Between Bubble Sort and Selection Sort

Conclusion

Bubble sort and selection sort are simple comparison-based sorting algorithms ideal for teaching sorting fundamentals. Bubble sort is stable and easy but slow due to excessive swaps. Selection sort performs fewer swaps and is more efficient but is not stable and still has quadratic time complexity. Neither algorithm is suitable for large datasets, but they are excellent for learning basic sorting mechanisms.

Bubble Sort and Selection Sort

1. Which sorting algorithm is stable?

1. Bubble Sort
2. Selection Sort
3. Both
4. None

2. Which sorting algorithm performs fewer swaps?

1. Bubble Sort
2. Selection Sort
3. Both perform equal swaps
4. None

3. Best case time complexity of Bubble Sort is:

1. O(n²)
2. O(1)
3. O(n)
4. O(log n)

4. In selection sort, which element is selected during each iteration?

1. Middle element
2. Largest element only
3. Smallest (or largest) element in unsorted part
4. Random element

5. Bubble sort compares:

1. Adjacent elements
2. Random elements
3. First and last only
4. None