How does Local Binary Pattern return an image?

Question

I'm trying to understand how scikit-image's local_binary_pattern() function works. Let's take the simplest setup: input is a grayscale image, radius = 1, n_points = 4, method = "uniform". How does this output an image?

From what I understand, there's a sliding 3x3 window that passes through the whole image. At each location, take the value of the center pixel and compare it to the values of the pixels above, left, below and right of the center pixel. Each may be less than or greater than the value of the center pixel. That's 2^4 = 16 possibilities. Make a histogram of how often each of the 16 possibilities occurs.

The problem is that this is a histogram, not an image. So why does local binary pattern return an image?

I asked someone about this, and he said maybe they don't make the histogram, and instead record the information about which pixels are greater than or less than the center as a length 4 binary vector. This can then be converted into an integer between 0 and 15 in the obvious way. Do this for all the pixels, and the result can then be interpreted as a greyscale image, with 16 levels. Ok, but this conversion necessarily depends on the order in which the neighboring pixels (above, left, below, right) are taken. So why does the documentation say that the "uniform" setting is rotation invariant?

Answer 1

Q:
"why does the documentation say that the "uniform" setting is rotation invariant?"

the rotation-independence part is well explained here :

Groups of continuous black or white pixels are considered “uniform” patterns that can be interpreted as corners or edges. If pixels switch back-and-forth between black and white pixels, the pattern is considered “non-uniform”.

In use, the rotational independence is warranted "grid-wise", as addition ( algebraic sum of values ) is commutative, that is order independent, as explained here :

"(...)
The rule for finding LBP of an image is as follows:

1) Set a pixel value as center pixel.
2) Collect its neighbourhood pixels (Here I am taking a 3 x 3 matrix so; total number of neighbourhood pixel is 8)
3) Threshold it’s neighbourhood pixel value to 1 if its value is greater than or equal to centre pixel value otherwise threshold it to 0.
4) After thresholding, collect all threshold values from neighbourhood either clockwise or anti-clockwise. The collection will give you an 8-digit binary code. Convert the binary code into decimal.
5) Replace the center pixel value with resulted decimal and do the same process for all pixel values present in image.
(...)"

Visually, for each pixel we do this :

Take the sum ( performed clockwise TLBR here ;o) ) :

  1 x 2^7
+ 1 x 2^6
+ 1 x 2^5
+ 0 x 2^4
+ 0 x 2^3
+ 0 x 2^2
+ 0 x 2^1
+ 1 x 2^0 
= 128 + 64 + 32 + 0 + 0 + 0 + 0 + 1
= 225

Finally, the sum gets assigned to the pixel, for which it was calculated by LBP-method. This is why the result is a piecewise-(pixel-wise)-computed transformed image :

This, per-pixel produced transformation is the answer to your original question :

Q :
"How does Local Binary Pattern return an image?"

Histograms are just helpers to represent relative frequencies of occurences of per-pixel computed LBP-sums, which thus carry some visually percievable representation of which 3x3-LBP-sums-("patterns") are less or more frequent in the whole original picture, thus helping to assume about texture/pattern (di)similarities, when algorithmically detecting (some phenomenon-under-study) or comparing visual scenes

Answer 2

This can then be converted into an integer between 0 and 15 in the obvious way. Do this for all the pixels, and the result can then be interpreted as a greyscale image, with 16 levels. Ok, but this conversion necessarily depends on the order in which the neighboring pixels (above, left, below, right) are taken. So why does the documentation say that the "uniform" setting is rotation invariant?

What you're describing is the way that method='default' works. The method='default' approach assigns a weight of 2 ** i to each point, so it matters what position the point is in. You're correct that this is not invariant to order. However, method='uniform' does something different.

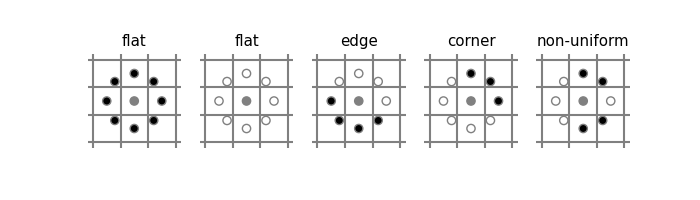
What uniform does is the following process:

1. First, compare each sampled point and compare it to the center point. For each sampled point, record a value in the signed_texture array. This value is 1 if the point is greater than or equal to the center point, and 0 otherwise.
2. Check if the point is uniform. This is defined as less than 3 changes between 0 and 1 while iterating over the signed_texture array.
3. If the point is uniform, output the sum of the signed_texture array. This will be a number between 0 and P inclusive.
4. Otherwise, if the point is non-uniform, output P + 1.

Since the number of transitions between 0 and 1 is rotation invariant, and the count of how many points are greater than the center point is also rotation invariant, the result is rotation invariant.

Below is a program that computes LBP using a simplified, pure Python, algorithm.

from skimage import data
from skimage.feature import local_binary_pattern
import numpy as np
import matplotlib.pyplot as plt
plt.gray()

image = data.brick()


def get_texture_values(image, r, c, rows, cols, offsets):
    """Given an image and a central point, sample points around that point."""
    texture = []
    for offset in offsets:
        offset_r, offset_c = offset
        offset_r_abs = offset_r + r
        offset_c_abs = offset_c + c
        if not (0 <= offset_r_abs < rows):
            texture.append(0)
        elif not (0 <= offset_c_abs < cols):
            texture.append(0)
        else:
            texture.append(image[offset_r_abs, offset_c_abs])
    return texture


def uniform(signed_texture, P):
    # This gets run once per pixel
    changes = 0
    for i in range(P - 1):
        changes += (signed_texture[i] - signed_texture[i + 1]) != 0
    result = 0
    if changes <= 2:
        for i in range(P):
            result += signed_texture[i]
    else:
        result = P + 1
    return result
    

def default(signed_texture, P):
    # This gets run once per pixel
    result = 0
    for i in range(P):
        result += signed_texture[i] * 2 ** i
    return result


def lbp_simplified(image, method='uniform'):
    rows, cols = image.shape
    P = 4  # Note: if you change this you must change offsets as well

    # Note: the actual local_binary_pattern allows fractional offsets
    # by doing bilinear interpolation. For simplicity, this has been
    # ignored.
    offsets = [
        [0, 1],
        [-1, 0],
        [0, -1],
        [1, 0],
    ]
    ret = np.zeros_like(image, dtype='float64')
    method_func = {
        'uniform': uniform,
        'default': default,
    }[method]
    for r in range(rows):
        for c in range(cols):
            value_here = image[r, c]
            texture = get_texture_values(image, r, c, rows, cols, offsets)
            signed_texture = [int(texture_value >= value_here) for texture_value in texture]
            ret[r, c] = method_func(signed_texture, P)
    return ret


# Check if lbp_simplified(image, method='uniform') is correct
reference_output = local_binary_pattern(image, P=4, R=1, method='uniform')
assert np.allclose(lbp_simplified(image, method='uniform'), reference_output)

# Plot uniform
plt.title("LBP uniform")
plt.imshow(lbp_simplified(image, method='uniform'))
plt.colorbar()
plt.show()

# Check if lbp_simplified(image, method='default') is correct
reference_output = local_binary_pattern(image, P=4, R=1, method='default')
assert np.allclose(lbp_simplified(image, method='default'), reference_output)

# Plot default
plt.title("LBP default")
plt.imshow(lbp_simplified(image, method='default'))
plt.colorbar()
plt.show()

The full details of how this works can be found here.

So why does local binary pattern return an image?

Essentially, this program evaluates default() or uniform() on each individual pixel, and the result of this is a number. The result is an array of the same size as the original image. This can be interpreted as an image.