You can use sum types to represent the entire hierarchy, without losing structure. Something like this would do it:
data Shape = IsPoint Point
| IsLine Line
| IsPolygon Polygon
data Point = Point { x :: Int, y :: Int }
data Line = Line { a :: Point, b :: Point }
data Polygon = IsTriangle Triangle
| IsQuad Quad
| ...
And so on. The basic pattern is you translate each OO abstract class into a Haskell sum type, with each of its immediate OO subclasses (that may themselves be abstract) as variants in the sum type. The concrete classes are product/record types with the actual data members in them.1
The thing you lose compared to the OOP you're used to by modeling things this way isn't the ability to represent your hierarchy, but the ability to extend it without touching existing code. Sum types are "closed", where OO inheritance is "open". If you later decide that you want a Circle option for Shape, you have to add it to Shape and then add cases for it everywhere you pattern match on a Shape.
However, this kind of hierarchy probably requires fairly liberal downcasting in OO. For example, if you want a function that can tell if two shapes intersect that's probably an abstract method on Shape like Shape.intersects(Shape other), so each sub-type gets to write its own implementation. But when I'm writing Rectangle.intersects(Shape other) it's basically impossible generically, without knowing what other subclasses of Shape are out there. I'll have to be using isinstance checks to see what other actually is. But that actually means that I probably can't just add my new Circle subclass without revisiting existing code; an OO hierarchy where isinstance checks are needed is de-facto just as "closed" as the Haskell sum type hierarchy is. Basically pattern matching on one of the sum-types generated by applying this pattern is the equivalent of isinstancing and downcasting in the OO version. Only because the sum types are exhaustively known to the compiler (only possible because they're closed), if I do add a Circle case to Shape the compiler is able to tell me about all the places that I need to revisit to handle that case.2
If you have a hierarchy that doesn't need a lot of downcasting, it means that the various base classes have substantial and useful interfaces that they guarantee to be available, and you usually use things through that interface rather than switching on what it could possibly be, then you can probably use type classes. You still need all the "leaf" data types (the product types with the actual data fields), only instead of adding sum type wrappers to group them up you add type classes for the common interface. If you can use this style of translation, then you can add new cases more easily (just add the new Circle data type, and an instance to say how it implements the Shape type class; all the places that are polymorphic in any type in the Shape class will now handle Circles as well). But if you're doing that in OO you always have downcasts available as an escape hatch when it turns out you can't handle shapes generically; with this design in Haskell it's impossible.3
But my "real" answer to "how do I represent OO type hierarchies in Haskell" is unfortunately the trite one: I don't. I design differently in Haskell than I do in OO languages4, and in practice it's just not a huge problem. But to say how I'd design this case differently, I'd have to know more about what you're using them for. For example you could do something like represent a shape as a Point -> Bool function (that tells you whether any given point is inside the shape), and having things like circle :: Point -> Int -> (Point -> Bool) for generating such functions corresponding to normal shapes; that representation is awesome for forming composite intersection/union shapes without knowing anything about them (intersect shapeA shapeB = \point -> shapeA point && shapeB point), but terrible for calculating things like areas and circumferences.
1 If you have abstract classes with data members, or you have concrete classes that also have further subclasses you can manually push the data members down into the "leaves", factor out the inherited data members into a shared record and make all of the "leaves" contain one of those, split a layer so that you have a product type containing the inherited data members and a sum type (where that sum type then "splits" into the options for the subclasses), stuff like that.
2 If you use catch-all patterns then the warning might not be exhaustive, so it's not always bullet proof, but how bullet proof it is is up to how you code.
3 Unless you opt into runtime type information with a solution like Typeable, but that's not an invisible change; your callers have to opt into it as well.
4 Actually I probably wouldn't design a hierarchy like this even in OO languages. I find it doesn't turn out to be as useful as you'd think in real programs, hence the "favour composition over inheritance" advice.
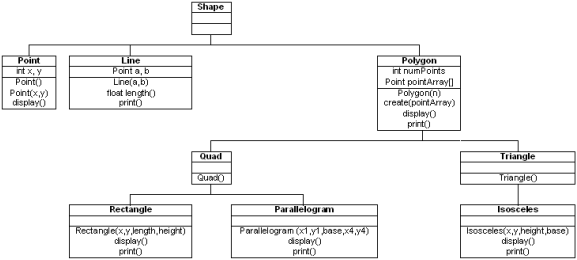
Shapeoffers no common behaviour, so the first step should be to dismantle the hierarchy.data Polygon = Quad Quad | ...; data Quad = Rectangle Point Point Length Length | Parallelogram Point Point Length Length Length; essentially each node is a the datatype containing nodes below it; and the constructor injecting that datatype into nodes above it.