Relations in Mathematics

A relation in Mathematics is defined as the relationship between two sets. If we are given two sets, set A and set B, and set A has a relation with set B, then each value of set A is related to a value of set B through some unique relation. Here, set A is called the domain of the relation, and set B is called the range of the relation.

Example of a Relation

Suppose there are two sets X = {4, 36, 49, 50} and Y = {1, -2, -6, -7, 7, 6, 2}. A relation R states that

"(x, y) is in the relation R if x is a square of y" can be represented using ordered pairs,

• R = {(4, -2), (4, 2), (36, -6), (36, 6), (49, -7), (49, 7)}

Also, the image added below shows two sets, A and B, and the relation between them.

• Set A = {x, y, z}
• Set B = {1, 2, 3}

Representation of Relations

In mathematics or set theory we can represent the relation using different techniques, and the two important ways to represent the set are,

• Set Builder Notation
• Roaster Notation

Set Builder Notation

If a relation between two sets is represented using the logical formula, then this type of representation is called the set builder notation.

For example, if we are given two sets, set X = {2, 4, 6} and set Y = {4, 8, 12}. Then, on observing clearly, we can see that each element of set Y is twice each element of set X the relation between them is,

R {(a, b): b is twice of a, a ∈ X, b ∈ Y}

Roaster Form

Roaster form is another way of representing a relation. In roaster form, we use ordered pairs to represent the relation.

For example, if we are given two sets, set X = {2, 4, 6} and set Y = {4, 8, 12}. Then the relation between set X and set Y is represented using the relation R such that,

R = {(2, 4), (4, 8), (6, 12)}

Types of Relation

• Empty Relation
• Reflexive Relation
• Symmetric Relation
• Transitive Relation
• Equivalence Relation
• Universal Relation
• Identity Relation
• Inverse Relation

Graphing Relations

Relations can be easily represented on the graphs, and representing them on graphs is an easy way of explaining them. The ordered pair in a relation represents a coordinate that can be plotted on the Cartesian coordinate system. We can easily graph the relation by following the steps added below.

• Substitute x with random numerical values in the relation.
• Find the corresponding y value of the respective x value.
• Write the ordered pair such that, {(x, y)}
• Plot these points and join them to find the required curve.

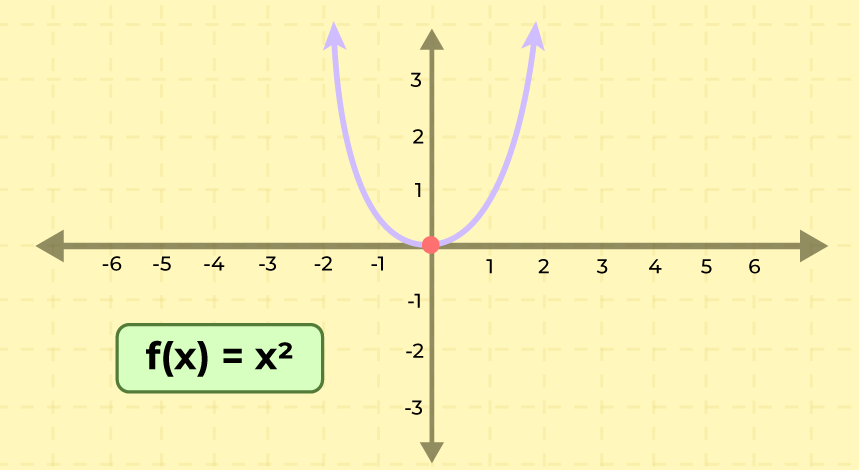
The graph of the relation y = x² is added below,

Importance in Computer Science

Relations are widely used in computer science, often without explicitly calling them “relations.” Some key applications include:

Databases (Relational Model)

• The term relational database comes directly from the mathematical concept of a relation.
• A database table is a set of tuples — exactly what a relation is in set theory.

Graphs and Networks

• A graph can be seen as a relation between vertices.
• In an undirected graph, the relation is symmetric.
• In a directed graph, the relation is not necessarily symmetric.

State Machines

• In automata theory, the transition function is a relation between states and inputs to next states.

Other Applications

• Data Structures: Adjacency matrices and adjacency lists in graphs are ways to store relations between nodes.
• Information Retrieval: Search engines model the relation between documents and keywords.

Solved Examples of Relations

Question 1: Find the inverse relation of R = {(1, 3), (2, 4), (3, 5)}

Solution:

Inverse relation is defined as R^-1 = {(y, x): (x, y) ∈ R}

Given,
R = {(1, 3), (2, 4), (3, 5)}

Inverse relation of R is R^-1 then,
R^-1 = {(3, 1), (4, 2), (5, 3)}

Question 2: Find the inverse relation of R = {(a, x), (b, y), (c, z)}

Solution:

Inverse relation is defined as R^-1 = {(y, x): (x, y) ∈ R}

Given,
R = {(a, x), (b, y), (c, z)}

Inverse relation of R is R-1 then,
R^-1 = {(x, a), (y, b), (z, c)}

Question 3: Is the relation R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1), (2, 3), (3, 2)} on set A = {1, 2, 3} an equivalence relation?

Solution:

No, it's not an equivalence relation. It's reflexive and symmetric, but not transitive.

Question 4: Find the domain and range of the relation R = {(1, 2), (2, 3), (3, 4), (4, 5)}.

Solution:

Domain = {1, 2, 3, 4}, Range = {2, 3, 4, 5}

Question 5: Is the relation R = {(x, y) | x² + y² = 25} on the set of real numbers a function?

Solution:

No, it's not a function. For example, (0, 5) and (0, -5) are both in the relation.

Question 6: Find the inverse of the relation R = {(1,1), (2,4), (3,9), (4,16)}.

Solution:

R⁻¹ = {(1, 1), (4, 2), (9, 3), (16, 4)}

Question 7: Determine if the relation R = {(x, y) | x - y is even} on the set of integers is an equivalence relation.

Solution:

Yes, it's an equivalence relation. It's reflexive, symmetric, and transitive.

Question 8: Find the composition R ∘ S for R = {(1, 2), (2, 3), (3, 4)} and S = {(1, 1), (2, 2), (3, 3), (4, 4)}.

Solution:

R ∘ S = {(1, 2), (2, 3), (3, 4)}

Question 9: Is the relation R = {(a, b) | a is a multiple of b} on the set of positive integers transitive?

Solution:

Yes, it's transitive.

Question 10: Find the reflexive closure of R = {(1, 2), (2, 3), (3, 1)} on set A = {1, 2, 3}.

Solution:

Reflexive closure = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (3, 1)}

Unsolved Examples of Relations

Question 1: Find the inverse relation of R = {(2, 5), (3, 6), (4, 7)}.

Question 2: Find the inverse relation of R = {(p, q), (r, s), (t, u)}.

Question 3: Determine whether the relation R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)} on the set A = {1, 2, 3} is reflexive, symmetric, and transitive.

Question 4: Find the domain and range of R = {(2, 4), (3, 9), (4, 16), (5, 25)}.

Question 5: Find the inverse of the relation R = {(1, 2), (2, 3), (3, 4), (4, 5)}.

Question 7: Check whether the relation R = {(x, y)∣x + y is even} on the set of integers is an equivalence relation.

Question 9: Determine whether the relation R = {(a, b)∣a divides b} on the set of positive integers is transitive.

Question 6: Find the inverse of the relation R = {(1, 2), (2, 3), (3, 4), (4, 5)}.

Question 8: Find the composition of relations R∘S, where R = {(1, 2), (2, 3), (3, 1)} and S = {(1, 3), (2, 1), (3, 2)}.

Question 10: Find the reflexive closure of R = {(a, b), (b, c)} on the set A={a, b, c}.

Related Articles

• Types Of Sets
• Relation and Function
• Types of Functions
• Representation of Relation in Graphs and Matrices
• Relations in Mathematics