Introduction to Statistics
Last Updated :
03 Oct, 2025
Statistics is a branch of mathematics concerned with collecting, organizing, analyzing, and interpreting numerical data. It is recognized as a distinct scientific discipline due to its broad applications across numerous fields, including science, economics, healthcare, and social sciences.
- Helps make sense of complex data through quantitative models.
- Plays a critical role in decision-making in fields like weather forecasting, stock market analysis, insurance, and data science.
Here are some examples of statistical concepts in action:
Statistics Terminologies
Some of the most common terms you might come across in statistics are:
- Population: It is actually a collection of a set of individual objects or events whose properties are to be analyzed.
- Sample: It is the subset of a population.
- Variable: It is a characteristic that can have different values.
- Parameter: It is numerical characteristic of population.
Types of Statistics
Statistics is the study of data; when we talk about properties of data, it comes under descriptive statistics. Meanwhile, the study of concluding data comes under inferential statistics.
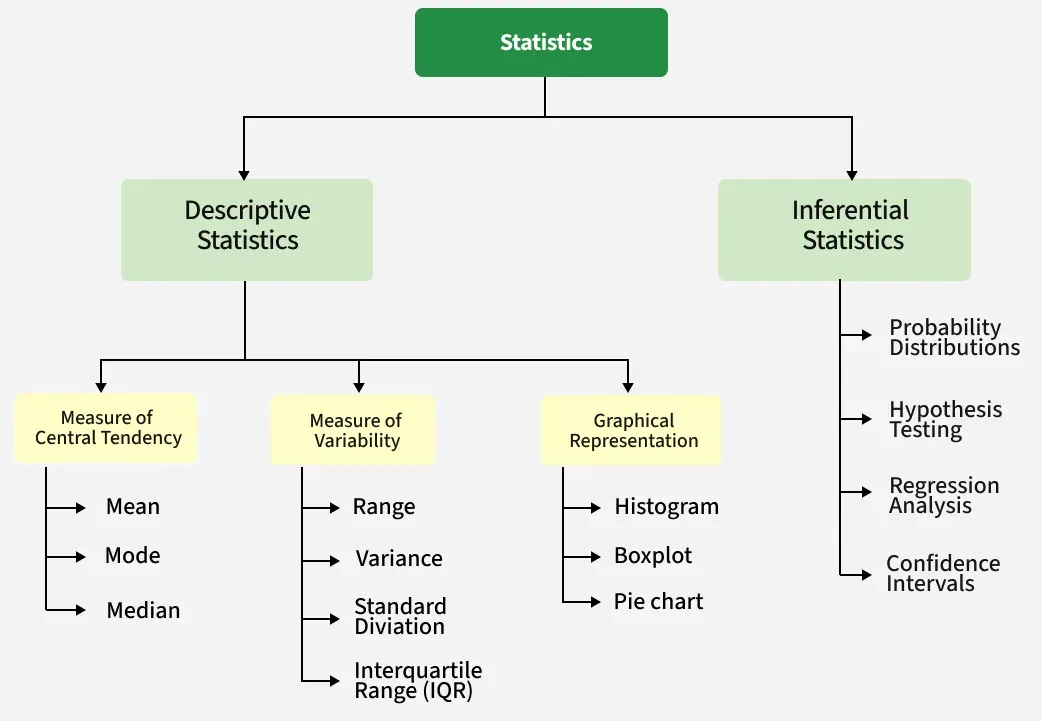 Types of statistics
Types of statistics
Descriptive Statistics
Descriptive statistics uses data that describes the population either through numerical calculations, graphs, or tables. It provides a graphical summary of data.
It is simply used for summarizing objects, etc. There are two categories in this, as follows.
- Measure of Central Tendency
- Measure of Variability
Measure of Central Tendency
Measure of central tendency is also known as a summary statistic that is used to represent the center point or a particular value of a data set or sample set. In statistics, three common measures of central tendency are:
1. Mean
Mean is the measure of the average of all values in a sample set. The size of the data set is calculated using the following formula:
Mean = ∑xn∑nx
2. Median
Median is the middle value in a data set when the numbers are arranged in ascending or descending order.
- If there is an odd number of values, the median is the middle one.
- If there is an even number of values, the median is the average of the two middle numbers.
The formula used to calculate the median of the data set is:
If n is Even, Median = [(n/2)th term + {(n/2 )+ 1}th term]/2
If n is Odd, Median = \frac{(n+1)}{2}
3. Mode
Mode is the value that appears most frequently in a data set.
- A data set may have no mode, one mode (unimodal), two modes (bimodal), or more than two modes (multimodal).
Measure of Variability
The measure of Variability is also known as the measure of dispersion and is used to describe variability in a sample or population. In statistics, there are three common measures of variability, as shown below:
1. Range of Data
It is a given measure of how to spread apart values in a sample set or data set.
Range = Maximum value - Minimum value
2. Variance
In probability theory and statistics, variance measures a data set's spread or dispersion. It is calculated by averaging the squared deviations from the mean. Variance is usually represented by the symbol σ2.
Variance measures variability. The more spread out the data, the greater the variance compared to the average.
3. Standard Deviation
Standard Deviation is a measure of how widely distributed a set of values is from the mean. It compares every data point to the average of all the data points.
Standard Deviation Formula
s = \sqrt{\frac{1}{n-1}\sum_{i=1}^n (x_i - \bar{x})^2}
Where:
- s is Population Standard Deviation
- xi is the ith observation
- x̄ is the Sample Mean
- N is the Number of Observations
4. Interquartile Range (IQR)
The Interquartile Range is a measure of statistical dispersion, or how spread out the data points are in a data set. It is the range between the first quartile (Q1) and the third quartile (Q3) of a data set, which represents the middle 50% of the data.
Formula for IQR:
IQR = Q3 − Q1
Where:
- Q1 is the first quartile (25th percentile), which is the median of the lower half of the data.
- Q3 is the third quartile (75th percentile), which is the median of the upper half of the data.
Inferential Statistics
Inferential Statistics makes inferences and predictions about the population based on a sample of data taken from the population. It generalizes a large dataset and applies probabilities to conclude.
It is simply used for explaining the meaning of descriptive statistics. It is simply used to analyze, interpret results, and draw conclusions. Inferential Statistics is mainly related to and associated with hypothesis testing, whose main target is to reject the null hypothesis.
Types of Inferential Statistics
Various types of inferential statistics are used widely nowadays and are very easy to interpret. These are given below:
Hypothesis Testing
Hypothesis testing is a type of inferential procedure that takes the help of sample data to evaluate and assess the credibility of a hypothesis about a population.
Inferential statistics are generally used to determine how strong a relationship is within the sample. However, it is very difficult to obtain a population list and draw a random sample. Inferential statistics can be done with the help of various steps as given below:
- Obtain and start with a theory.
- Generate a research hypothesis.
- Operationalize or use variables
- Identify or find out the population to which we can apply study material.
- Generate or form a null hypothesis for these populations.
- Collect and gather a sample of children from the population and simply run a study.
- Then, perform all tests of statistical to clarify if the obtained characteristics of the sample are sufficiently different from what would be expected under the null hypothesis so that we can be able to find and reject the null hypothesis.
Data in Statistics
Data is the collection of numbers, words, or anything that can be arranged to form meaningful information. There are various types of data in the statistics that are added below.
Types of Data
Various types of Data used in statistics are:
- Qualitative data: is the descriptive data of any object. For example, Sam is tall, adam is thin, etc.
- Quantitative data: is the numerical data of any object. For example, he ate three burgers, and we are five friends.
Types of Quantitative Data
We have two types of quantitative data that include,
- Discrete Data: The data that has a fixed value is called discrete data and can easily be counted.
- Continuous Data: The data that has no fixed value and has a range of values is called continuous data. It can be measured.
Representation of Data
We can easily represent the data using various graphs, charts, or tables. The various types of representing data sets are:
Read more about the Representation of Data in Statistics from Types of Graphs in Statistics
Models of Statistics
Various models of Statistics are used to measure different forms of data. Some of the models of statistics are added below:
Related Articles
Solved Problems - Statistics
Example 1: Find the mean of the data set.
Solution:
Mean = (Σf ixi)/Σfi
Σfixi = (6 + 12 + 20 + 40) = 78, and
Σfi = 16
⇒ Mean = 78/16 = 4.875
Example 2: Find the median of the data set.
Cars | Mileage | Cylinder |
|---|
Swift | 21.3 | 3 |
Verna | 20.8 | 2 |
Santra | 19 | 5 |
| i-20 | 15 | 4 |
Solution:
Data in order: 15, 19, 20.8, 21.3
⇒ Median = (20.8 + 19) /2 = 39.8/2
⇒ Median = 19.9
Example 3: Find the Standard Deviation of 4, 7, 10, 13, and 16.
Solution:
Given,
- xi = 4, 7, 10, 13, 16
- N = 5
Σxi = (4 + 7 + 10 + 13 + 16) = 50
⇒ Mean(μ) = Σxi/N = 50/5 = 10
Standard Deviation = √(σ) = √{∑i = 1n (xi - μ)}/N
⇒ SD = √{1/5[(4 - 10)2 + (7 - 10)2 + (10 - 10)2 + (13 - 10)2 + (16 - 10)2]}
⇒ SD = √{1/5[36 + 9 + 0 + 9 + 36] = √{1/5[90]} = √18
Explore
Basic Arithmetic
Algebra
Geometry
Trigonometry & Vector Algebra
Calculus
Probability and Statistics
Practice
My Profile