Fractions - Definition, Types and Examples
Last Updated :
05 Sep, 2025
Fractions are numerical expressions used to represent parts of a whole or ratios between quantities.
Example: If an apple is divided into 4 equal parts, and one part is taken out, thus the fraction representing the taken out part is 1/4 as one part is taken out of 4 equal parts.
If 3 parts are taken then the fraction representing the taken out part will be 3/4.
Some common real life examples of fractions are:
Parts of a Fraction
If we divide anything into some equal parts, then a fraction consists of two main parts and a fraction line:
- Numerator: The number at the top of the fraction represents the number of parts being considered.
- Vinculum: The line that separates the numerator and denominator is also called the fraction line.
- Denominator: The number at the bottom of the fraction, representing the total number of equal parts into which the whole is divided.
Example:
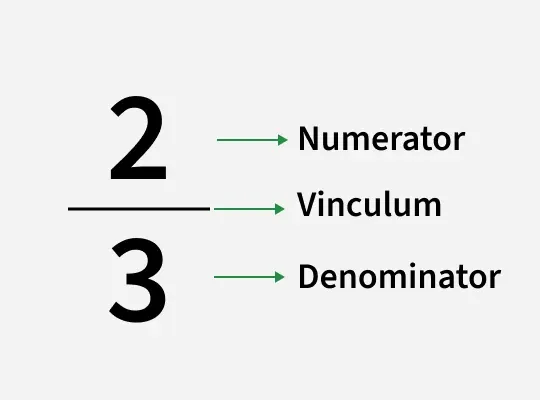 Parts of a Fraction
Parts of a FractionUse the following tools to understand the fraction better:
Types of Fractions
There are seven types of fractions. They are categorized based on their numerator and denominator, and they are:
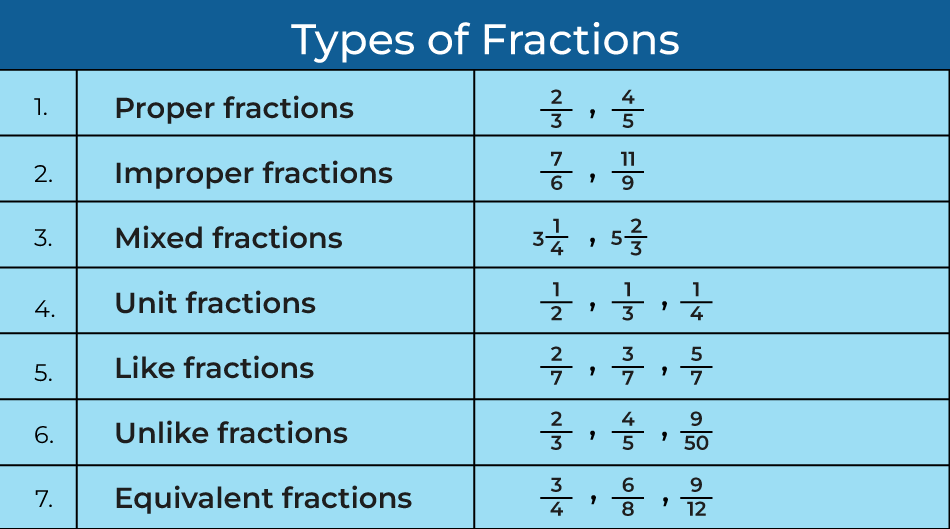 7 types of fractions
7 types of fractionsLet's read them in detail:
1) Proper Fraction: Fractions in which the numerator value is less than the denominator value.
2) Improper Fractions: Fractions in which the numerator value is greater than the denominator value.
3) Mixed Fractions: Fraction that consists of a whole number with a proper fraction.
4) Like Fractions: Fractions whose denominators are the same are known as like fractions
5) Unlike Fractions: Fractions whose denominators are different are called unlike fractions.
6) Unit Fraction: A Fraction with 1 as a numerator is known as a Unit Fraction. All unit fractions are proper fractions since all unit fractions have 1 in the numerator, which is less than the denominator.
7) Equivalent Fractions: Fractions that result in the same value after simplification.
➣ Read more about Like and Unlike Fractions.
Fractions on a Number Line
Fractions on a number line are shown between two integers. The whole is divided into equal parts based on the denominator, and the numerator shows the fraction's position.
Example

➣ Check- Fraction Quiz
Fractions Operations
Some of the basic arithmetic operations that can be performed on the fractions are:
Fractions- Addition and Subtraction
Fractions can be added and subtracted like simple numbers, but only after making their denominators the same.
Steps to add or subtract fractions:
- Find the Least Common Denominator (LCD) of the fractions.
- Convert each fraction to an equivalent fraction with the LCD as the denominator.
- Add or subtract the numerators while keeping the denominator the same.
Example: \frac{2}{5} + \frac{1}{3} \ \text{and}, \frac{2}{5} - \frac{1}{3}
- LCD of 5 and 3 is 15.
- Convert: 2/5 = 6/15, 1/3 = 5/15
- Add: 6/15 + 5/15 = 11/15
- Subtract: 6/15 - 5/15 = 1/15
Fraction Multiplication and Division
Fraction division and multiplication are straightforward.
Steps to multiply fractions:
- Multiply the numerators together.
- Multiply the denominators together.
- Simplify the resulting fraction if possible.
Example: \frac{2}{5} \times \frac{1}{3}
\frac{2}{5} \times \frac{1}{3} = \frac{2}{15}
Steps to divide fractions:
- Flip (find the reciprocal of) the second fraction.
- Multiply the first fraction by the reciprocal of the second fraction.
- Simplify the resulting fraction if possible.
Example: \frac{2}{5} \div \frac{1}{3}
\dfrac{2}{5} \div \dfrac{1}{3}
= \dfrac{2}{5} \times \dfrac{3}{1}
= \frac{6}{5} \ = 1\frac{1}{5}
Fraction Worksheets
Practice the fractions with these useful worksheets on fractions.
Properties of Fractions
There are some important properties of fractions similar to whole numbers, natural numbers, etc. Let's take a look at those properties:
| Property | Description | Example |
|---|
Commutative
(Addition & Multiplication) | The order of adding or multiplying fractions doesn't
change the result. | Addition: a/b + c/d = c/d + a /b
Multiplication: a/b × c/d = c/d × a /b |
Associative
(Addition & Multiplication) | The way fractions are grouped in addition or
Multiplication doesn't change the result. | Addition: (a/b + c/d )+ e/f = a/b + (c/d )+ e/f )
Multiplication: (a/b × c/d) × e/f = a/b × (c/d × e/f) |
| Identity Element | For multiplication, the identity is 1 (multiplying a
fraction by 1 gives the same fraction). For in
addition, the identity element is incorrectly
noted as 0 in the statement; it should be that
adding 0 to a fraction doesn't change its value. | Multiplication: (a/b) ×1 =a/b
Addition: a/b+0 =a/b |
| Multiplicative Inverse | The reciprocal of a fraction, when multiplied by the original fraction, gives 1. | (a/b) × (b/a) = 1 |
| Distributive | Multiplying a fraction by the sum of two fractions equals the sum of each multiplied separately. | a/b × (c/d + e/f) = a/b × c/d + a/b× e/f |
➣ Related Articles
Solved Examples of Fractions
Example 1: Write two equivalent fractions of 3/39.
Solution:
Given, fraction : 3/39
Equivalent fraction by multiplying with the same number, lets multiply by 2:
= (3 × 2)/(39 × 2)
= 6/78
Equivalent fraction by division with the same number, here, both numerator and denominator are divisible by 3, dividing by 3:
= (3 ÷ 3)/(39 ÷ 3)
= 1/13
Example 2: In a class of 90 students, 1/3rd of the students do not like cricket. How many students like cricket?
Solution:
Fraction of students that do not like cricket = 1/3
Fraction of student that like cricket = 1 - 1/3
= (3 - 1)/3
= 2/3rd students like cricket.
Number of students that like cricket = 2/3 × 90
= (2 × 30)
= 60
Therefore, 60 students like cricket.
Example 3: What type of fraction is this - 1/2, 1/5, 1/7, 1/10, 1/3?
Soolution:
This is a Unit fraction because all the fractions have 1 as a numerator.
Example 4: If a recipe needs 3/4 cup of sugar and you want to make twice the quantity mentioned in the recipe, how much sugar do you need?
Solution:
Sugar needed for recipe = 3/4 cup
Sugar needed for half the recipe = 2 × 3/4
Required sugar = 2× 3/4 = 6/4
Therefore, we need 6/4 cup of sugar.
Practice Problems on Fractions
Use your knowledge to solve these fun questions on fractions.
Question 1: What fraction of the pizza is left?

Question 2: Order the following in ascending order: 1/2, 1, 4, 1/5, 1/3, and 1/5.
Question 3: What fraction of the blocks is green compared to white?
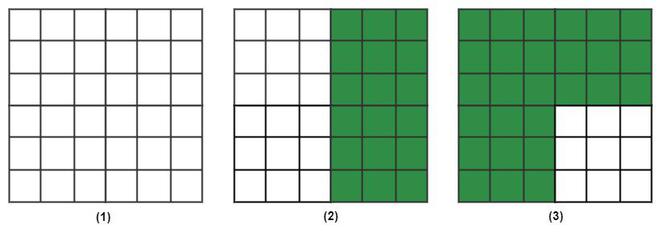
Question 4: Which among these is the greatest? 1/6, 1/4, 1/8, 1/16, 1/32?
Explore
Basic Arithmetic
Algebra
Geometry
Trigonometry & Vector Algebra
Calculus
Probability and Statistics
Practice
My Profile