Change of Order of Integration

When we evaluate a double integral, we add up the values of a function over a region by integrating one variable first and then the other. Sometimes, the given order of integration makes the problem harder to solve. In such cases, we can switch the order of integration—doing dx first and then dy, or vice versa.

The region of integration remains the same, but the limits of integration change. This rearrangement often simplifies the calculation.

The process of rewriting a double integral by interchanging the order of integration is called the change of order of integration.

Steps to follow the change of order of integration

1. Identify the variable limits

Look at the integral bounds. For example:

I = \int_{0}^{1} \int_{0}^{x} f(x,y) \, dx \, dy

• Outer integral: y goes from 0 to 1.
• Inner integral: x goes from 0 to y

2. From that, identify whether it's a horizontal strip or a vertical strip

The inner integral corresponds to the direction of the strip:

• dx → vertical strip (thin rectangle parallel to y-axis)
• dy → horizontal strip (thin rectangle parallel to x-axis)

Here, dx → vertical strip.

3. Trace the curve and identify the region :

Draw the region in the xy-plane using the bounds:

• y = 0 to 1
• x = y to 1

Shade the region. This is a triangle or trapezoid, depending on the bounds.

4. Change the strip: if horizontal, then vertical and vice versa

• If the original strip is vertical, change it to horizontal.
• The new integral will integrate in the opposite direction (dy first, then dx).

5. Find limits

Look at the shaded region:

• x goes from x to 1
• For fixed x, y goes from x to 1

So the new integral is:

I = \int_{0}^{2} \int_{0}^{x} f(x,y) \, dy \, dx

6. Integrate:

Integrate with the new limits step by step.

I = \int_{0}^{1} \int_{x}^{1} 1 \, dy \, dx= \int_{0}^{1} \big[y\big]_{y=x}^{y=1} \, dx= \int_{0}^{1} (1 - x) \, dx= \left[ x - \frac{x^2}{2} \right]_{0}^{1}= 1 - \frac{1}{2}= \frac{1}{2}

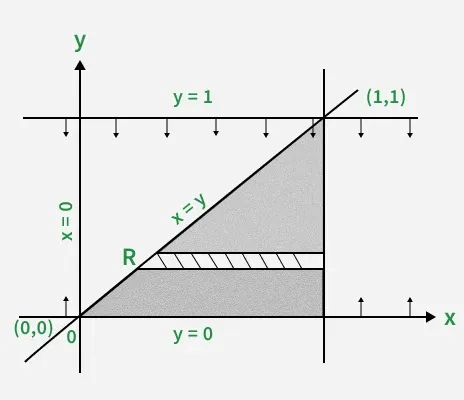
Example: Evaluate the integral by changing the order of integration:

\int_{0}^{2} \int_{0}^{x} f(x, y) \, dy \, dx

Solution:

Step 1 – Understand the limits:

• x goes from 0 to 2: 0 ≤ x ≤ 2.
• For each x, y goes from 0 to x: 0 ≤ y ≤ x.

Step 2 – Draw the Region:

• The region is a triangle under the line y = x, x = 2.

Step 3 – New Limits:

• Now, y goes from 0 to 2: 0 ≤ y ≤ 2.
• For each y, x goes from y to 2: y ≤ x ≤ 2.

Step 4 - New integral:

\int_{0}^{2} \int_{y}^{2} f(x, y) \, dx \, dy

Solved Question on change of order of Integration

Question 1: Change the order of integration and hence evaluate the \int_{0}^{a} \int_{x}^{a} f(x^{2}+y^{2}) \, dy \, dx

Solution:

It is correct form, given the order is dydx given y : x → a , x : 0 → a

the region is bounded by y = x, y = a x = 0 and x = a

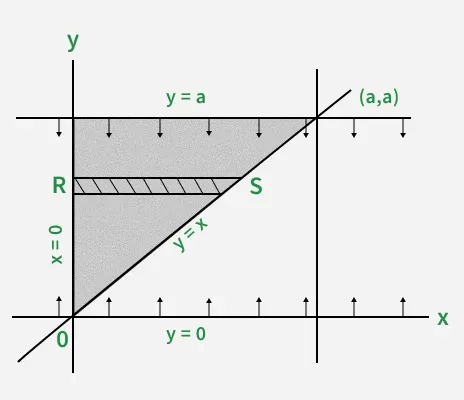
• x axis limit represnet the horizontal strip
• y axis limit represent vertical path

changed order is dxdy

• x : 0 → y
• y : 0 → a

\int_{0}^{a} \int_{x}^{a} f(x^{2}+y^{2}) \, dy \, dx = \int_{0}^{a} \int_{0}^{y} \left( \frac{x^{3}}{3} + y^{2}x \right) dx \, dy

= \int_{0}^{a} \left( \frac{y^{3}}{3} + y^{3} \right) dy

= \left[ \frac{y^{4}}{12} + \frac{y^{4}}{4} \right]_{0}^{a}

= \frac{a^{4}}{12} + \frac{a^{4}}{4}

= \frac{a^{4}}{3}\\

Question 2: Change the order of integration for \int_{0}^{4a} \int_\frac{x^2}{4a}^{2\sqrt{ax}} xy\, dy \, dx

Solution:

It is correct form.

Given order is dydx

The region is bounded by x² = 4ay , y² = 4ax

x = 0 and x = 4a

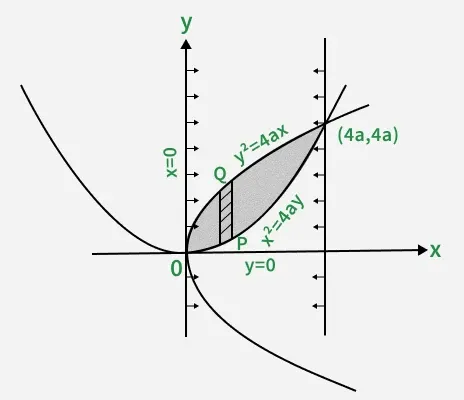
\int_{0}^{4a} \int_\frac{x^2}{4a}^{2\sqrt{ax}} xy\, dy \, dx = = \int_{0}^{4a} \int_{y^2/4a}^{2\sqrt{ay}} x y \, dx \, dy

= \int_{0}^{4a} \left[ \frac{x^2 y}{2} \right]_{x = y^2/4a}^{x = 2\sqrt{ay}} \, dy

= \int_{0}^{4a} \left[ (4 a y^2) - \frac{y^5}{32 a^2} \right] \, dy

=\left[ \frac{4 a y^3}{3} - \frac{y^6}{192 a^2} \right]_{0}^{4a}

= \frac{128 a^4}{3} - \frac{4096 a^4}{192}

= 64 a⁴

Unsolved Question on Change of Order of Integration

Question 1: Change of order of integration I = \int_{0}^{a} \int_{y}^{a} \frac{x}{x ^2 + y^2}\, dy \, dx and evaluate it.

Question 2: Change of order of integration I_2 = \int_{0}^{1} \int_{y^2}^{\sqrt{y}} e^{x^2} \, dx \, dy and evaluate it.

Question 3: Change of order of integration I_3 = \int_{0}^{3} \int_{0}^{x} \frac{\sin(y)}{x+y} \, dy \, dxand evaluate it.

Question 4: Change of order of integration I_4 = \int_{0}^{1} \int_{x}^{\sqrt{2x}} \frac{y}{1+y^2} \, dy \, dx and evaluate it.