In calculus, Lagrange’s Mean Value Theorem (LMVT) is a special theorem that connects the derivative of a function with its overall change on an interval. It tells us that if a function is continuous and differentiable, then there exists at least one point where the slope of the tangent is the same as the slope of the secant line.
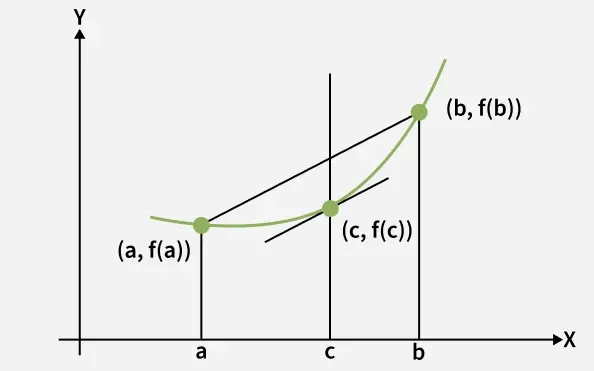 Lagrange's Mean Value Graph
Lagrange's Mean Value Graph
Formula used in Lagrange's Mean Value Theorem :
f'(c) = \frac{f(b) - f(a)}{b - a}
Statement
Lagrange’s Mean Value Theorem states that, for a function f(x) satisfying the following conditions,
- f(x) is continuous in the closed interval a ≤ x ≤ b, i.e., x∈[a, b].
- f(x) is differentiable in the open interval a < x < b, i.e., x∈(a, b).
Then, there exists a point c in the open interval a < c < b such that
f'(c) = \frac{f(b) - f(a)}{b - a}
Proof of Lagrange's Mean Value Theorem
To prove LMVT, consider the function f(x) and the auxiliary function g(x) defined by:
g(x) = f(x) - (\frac{f(b) - f(a)}{b - a}) (x -a)
- The function g(x) is continuous on [a, b] and differentiable on (a,b)
- At x = a, g(a) = f(a).
- At x = b, g(b) = f(b) - (\frac{f(b) - f(a)}{b - a}) (b − a) = f(b)−(f(b)−f(a)) = f(a).
Thus, g(a) = g(b), and by Rolle's Theorem, there exists a point c ∈ (a, b) such that g′(c) = 0.
Differentiating g(x):
g′(x) = f′(x) - \frac{f(b) - f(a)}{b - a}
Setting g′(c) = 0:
f′(c) = \frac{f(b) - f(a)}{b - a}
Hence, the theorem is proven.
Lagrange's Mean Value Theorem - Sample Problems
Example 1: Consider f(x) = x2 on the interval [1, 3].
Step 1: Verify the conditions:
f(x) = x2 is continuous on [1, 3] and differentiable on (1, 3).
Step 2: Calculate [f(b) - f(a)] / (b - a):
[f(3) - f(1)] / (3 - 1) = (9 - 1) / 2 = 4
Step 3: Find f'(x):
f'(x) = 2x
Step 4: Solve f'(c) = 4:
2c = 4
c = 2
Therefore, c = 2 satisfies the Mean Value Theorem.
Example 2: Consider f(x) = sin(x) on the interval [0, π/2].
Step 1: Verify the conditions:
sin(x) is continuous on [0, π/2] and differentiable on (0, π/2).
Step 2: Calculate [f(b) - f(a)] / (b - a):
[sin(π/2) - sin(0)] / (π/2 - 0) = (1 - 0) / (π/2) = 2/π
Step 3: Find f'(x):
f'(x) = cos(x)
Step 4: Solve cos(c) = 2/π:
c = arccos(2/π) ≈ 0.6435 radians
Therefore, c ≈ 0.6435 satisfies the Mean Value Theorem.
Example 3: Consider f(x) = ln(x) on the interval [1, e].
Step 1: Verify the conditions:
ln(x) is continuous on [1, e] and differentiable on (1, e).
Step 2: Calculate [f(b) - f(a)] / (b - a):
[ln(e) - ln(1)] / (e - 1) = (1 - 0) / (e - 1) = 1/(e - 1)
Step 3: Find f'(x):
f'(x) = 1/x
Step 4: Solve 1/c = 1/(e - 1):
c = e - 1
Therefore, c = e - 1 satisfies the Mean Value Theorem
Example 4: f(x) = x3 on the interval [0, 2]
f(x) = x3 on the interval [0, 2]
Step 1: f(x) = x3 is continuous on [0, 2] and differentiable on (0, 2).
Step 2: [f(2) - f(0)] / (2 - 0) = (8 - 0) / 2 = 4
Step 3: f'(x) = 3x2
Step 4: Solve 3c2 = 4
c = √(4/3) ≈ 1.15
Example 5: f(x) = ex on the interval [0, 1]
Step 1: ex is continuous on [0, 1] and differentiable on (0, 1).
Step 2: [f(1) - f(0)] / (1 - 0) = (e - 1) / 1 = e - 1
Step 3: f'(x) = ex
Step 4: Solve ec = e - 1
c = ln(e - 1) ≈ 0.54
Example 6: f(x) = cos(x) on the interval [0, π]
Step 1: cos(x) is continuous on [0, π] and differentiable on (0, π).
Step 2: [f(π) - f(0)] / (π - 0) = (-1 - 1) / π = -2/π
Step 3: f'(x) = -sin(x)
Step 4: Solve -sin(c) = -2/π
c = arcsin(2/π) ≈ 0.69
Example 7: f(x) = x2 - 3x + 2 on the interval [1, 4]
Step 1: x2 - 3x + 2 is continuous on [1, 4] and differentiable on (1, 4).
Step 2: [f(4) - f(1)] / (4 - 1) = [(16 - 12 + 2) - (1 - 3 + 2)] / 3 = 6/3 = 2
Step 3: f'(x) = 2x - 3
Step 4: Solve 2c - 3 = 2
c = 2.5
Example 8: f(x) = √x on the interval [1, 9]
Step 1: √x is continuous on [1, 9] and differentiable on (1, 9).
Step 2: [f(9) - f(1)] / (9 - 1) = (3 - 1) / 8 = 1/4
Step 3: f'(x) = 1 / (2√x)
Step 4: Solve 1 / (2√c) = 1/4
c = 4
Example 9: f(x) = x3 - x on the interval [-1, 2]
Step 1: x3 - x is continuous on [-1, 2] and differentiable on (-1, 2).
Step 2: [f(2) - f(-1)] / (2 - (-1)) = [(8 - 2) - (-1 + 1)] / 3 = 6/3 = 2
Step 3: f'(x) = 3x2 - 1
Step 4: Solve 3c2 - 1 = 2
3c2 = 3
c = ±1
Both c = 1 and c = -1 satisfy the theorem.
Example 10: f(x) = ln(x+1) on the interval [0, e-1]
Step 1: ln(x+1) is continuous on [0, e-1] and differentiable on (0, e-1).
Step 2: [f(e-1) - f(0)] / ((e-1) - 0) = [ln(e) - ln(1)] / (e-1) = 1 / (e-1)
Step 3: f'(x) = 1 / (x+1)
Step 4: Solve 1 / (c+1) = 1 / (e-1)
c+1 = e-1
c = e-2 ≈ 0.72
Practice Problems on Lagrange's Mean Value Theorem
Question 1: Find the value of c guaranteed by the Mean Value Theorem for f(x) = x2 + 2x on the interval [0, 3].
Question 2: Verify that f(x) = x3 satisfies the conditions of the Mean Value Theorem on [-1, 2], and find all values of c that satisfy the conclusion of the theorem.
Question 3: Determine whether there is a value of c that satisfies the Mean Value Theorem for f(x) = |x| on the interval [-2, 2].
Question 4: Find the value of c guaranteed by the Mean Value Theorem for f(x) = sin(x) on the interval [0, π/3].
Question 5: For f(x) = ex, find the value of c guaranteed by the Mean Value Theorem on the interval [ln 2, ln 5]
Question 6: Verify that f(x) = 1/x satisfies the conditions of the Mean Value Theorem on [1, 4], and find the value of c that satisfies the conclusion of the theorem.
Question 7: Find all values of c that satisfy the Mean Value Theorem for f(x) = x4 - 2x2 on the interval [-1, 1].
Question 8: Determine whether there is a value of c that satisfies the Mean Value Theorem for f(x) = tan(x) on the interval [0, π/4].
Question 9: For f(x) = ln(x2 + 1), find the value of c guaranteed by the Mean Value Theorem on the interval [0, 1].
Question 10: Verify that f(x) = cos(x) satisfies the conditions of the Mean Value Theorem on [0, 2π], and find all values of c in this interval that satisfy the conclusion of the theorem
Explore
Linear Algebra
Sequence & Series
Calculus
Probability & Statistics
Practice Questions
My Profile