Error Detection in Computer Networks
Last Updated :
25 Sep, 2025
Error detection in computer networks ensures that data is transmitted accurately without corruption. It works by adding extra (redundant) bits to data so the receiver can verify its correctness. If errors are found, the receiver discards the frame and requests retransmission.
- Detects errors caused by noise or interference.
- Uses redundant bits for consistency checking.
- Common methods: Parity Check, Checksum, CRC.
- Ensures data integrity and reliable communication.
Types of Errors
1. Single-Bit Error
A single-bit error refers to a type of data transmission error that occurs when one bit (i.e., a single binary digit) of a transmitted data unit is altered during transmission, resulting in an incorrect or corrupted data unit.
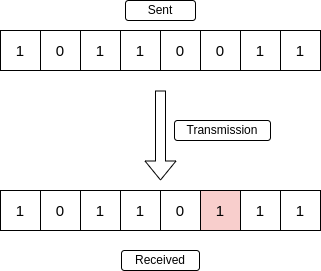 Single-Bit Error
Single-Bit Error2. Multiple-Bit Error
A multiple-bit error is an error type that arises when more than one bit in a data transmission is affected. Although multiple-bit errors are relatively rare when compared to single-bit errors, they can still occur, particularly in high-noise or high-interference digital environments.
 Multiple-Bit Error
Multiple-Bit Error3. Burst Error
When several consecutive bits are flipped mistakenly in digital transmission, it creates a burst error. This error causes a sequence of consecutive incorrect values.
 Burst Error
Burst ErrorError Detection Methods
To detect errors, a common technique is to introduce redundancy bits that provide additional information. Various techniques for error detection include:
- Simple Parity Check
- Two-Dimensional Parity Check
- Checksum
- Cyclic Redundancy Check (CRC)
1. Simple Parity Check
Simple bit parity is a simple error detection method that involves adding an extra bit to a data transmission. It works as:
- 1 is added to the block if it contains an odd number of 1’s, and
- 0 is added if it contains an even number of 1’s
This scheme makes the total number of 1’s even, that is why it is called even parity checking.
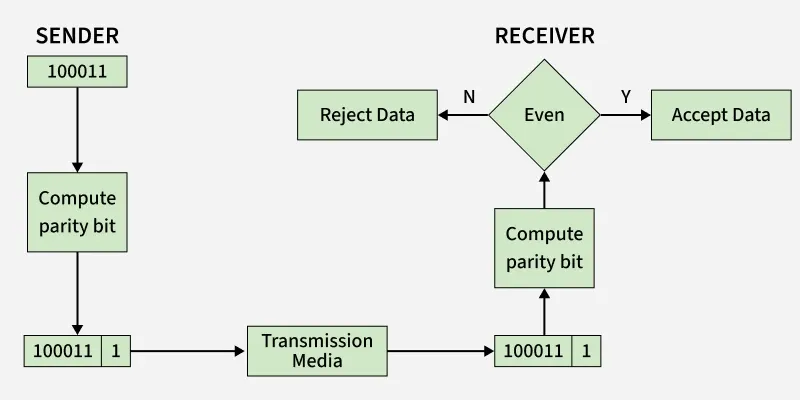 Simple Parity Check
Simple Parity CheckAdvantages of Simple Parity Check
- Simple parity check can detect all single bit error.
- Simple parity check can detect an odd number of errors.
- Implementation: Simple Parity Check is easy to implement in both hardware and software.
- Minimal Extra Data: Only one additional bit (the parity bit) is added per data unit (e.g., per byte).
- Fast Error Detection: The process of calculating and checking the parity bit is quick, which allows for rapid error detection without significant delay in data processing or communication.
- Single-Bit Error Detection: It can effectively detect single-bit errors within a data unit, providing a basic level of error detection for relatively low-error environments.
Disadvantages of Simple Parity Check
- Single Parity check is not able to detect even no. of bit error.
- For example: the Data to be transmitted is 101010. Codeword transmitted to the receiver is 1010101 (we have used even parity).
Let's assume that during transmission, two of the bits of code word flipped to 1111101.
On receiving the code word, the receiver finds the no. of ones to be even and hence no error, which is a wrong assumption.
2. Two-Dimensional Parity Check
Two-dimensional Parity check bits are calculated for each row, which is equivalent to a simple parity check bit. Parity check bits are also calculated for all columns, then both are sent along with the data. At the receiving end, these are compared with the parity bits calculated on the received data.
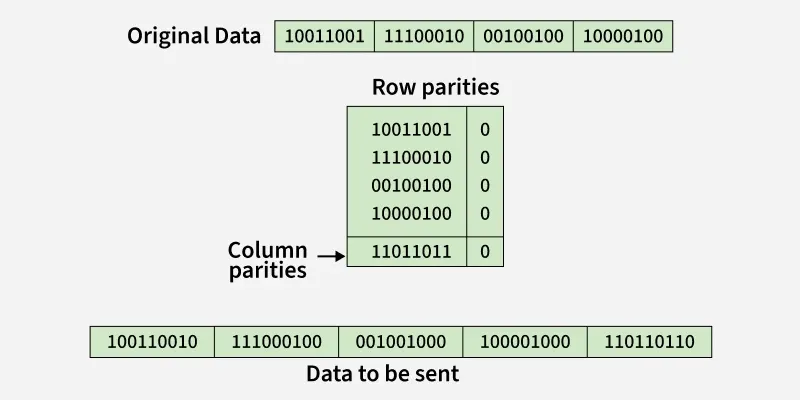 2-D Parity Check
2-D Parity Check
Advantages of Two-Dimensional Parity Check
- Two-Dimensional Parity Check can detect and correct all single bit error.
- Two-Dimensional Parity Check can detect two or three bit error that occur any where in the matrix.
Disadvantages of Two-Dimensional Parity Check
- Two-Dimensional Parity Check can not correct two or three bit error. It can only detect two or three bit error.
- If we have a error in the parity bit then this scheme will not work.
3. Checksum
Checksum error detection is a method used to identify errors in transmitted data. The process involves dividing the data into equally sized segments and using a 1's complement to calculate the sum of these segments. The calculated sum is then sent along with the data to the receiver. At the receiver's end, the same process is repeated and if all zeroes are obtained in the sum, it means that the data is correct.
Checksum - Operation at Sender's Side
- Firstly, the data is divided into k segments each of m bits.
- On the sender’s end, the segments are added using 1’s complement arithmetic to get the sum. The sum is complemented to get the checksum.
- The checksum segment is sent along with the data segments.
Checksum - Operation at Receiver's Side
- At the receiver’s end, all received segments are added using 1’s complement arithmetic to get the sum. The sum is complemented.
- If the result is zero, the received data is accepted; otherwise discarded.
 Checksum at Receiver 's and Sender's Side
Checksum at Receiver 's and Sender's Side
Read more about Checksum
4. Cyclic Redundancy Check (CRC)
- Unlike the checksum scheme, which is based on addition, CRC is based on binary division.
- In CRC, a sequence of redundant bits, called cyclic redundancy check bits, are appended to the end of the data unit so that the resulting data unit becomes exactly divisible by a second, predetermined binary number.
- At the destination, the incoming data unit is divided by the same number. If at this step there is no remainder, the data unit is assumed to be correct and is therefore accepted.
- A remainder indicates that the data unit has been damaged in transit and therefore must be rejected.
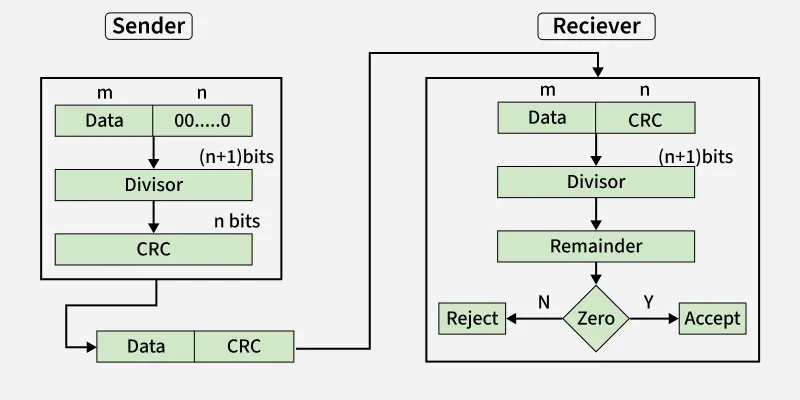 CRCCRC Working
CRCCRC Working
We have given dataword of length n and divisor of length k.
Step 1: Append (k-1) zero's to the original message
Step 2: Perform modulo 2 division
Step 3: Remainder of division = CRC
Step 4: Code word = Data with append k-1 zero's + CRC
Note:
- CRC must be k-1 bits
- Length of Code word = n+k-1 bits
Example: Let's data to be send is 1010000 and divisor in the form of polynomial is x3+1. CRC method discussed below.
 CRC Working
CRC Working
To learn about CRC in detail, refer to: Cyclic Redundancy Check(CRC)
Explore
Computer Network Basics
Physical Layer
Data Link Layer
Network Layer
Transport Layer
Session Layer & Presentation Layer
Application Layer
Advanced Topics
Practice
My Profile