Check if a Binary Tree is subtree of another binary tree | Set 1
Last Updated :
04 Oct, 2024
Given two binary trees, check if the first tree is a subtree of the second one. A subtree of a tree T(root1) is a tree S(root2) consisting of a node in T and all of its descendants in T. The subtree corresponding to the root node is the entire tree and the subtree corresponding to any other node is called a proper subtree.
Examples:
Input:
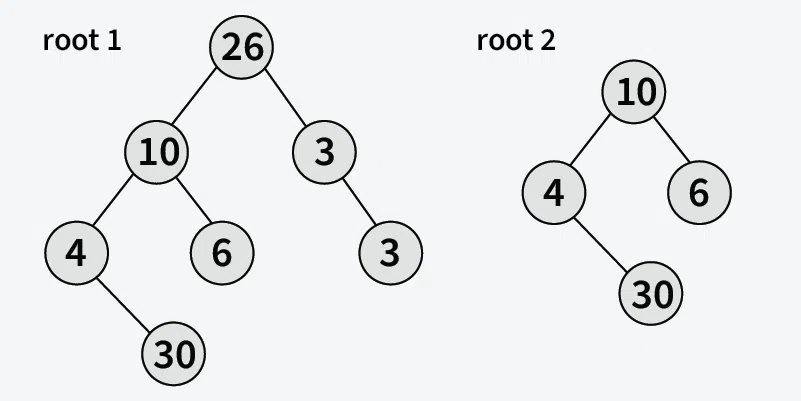
Output: True
Explanation: root2 is the subtree of root1.
Approach:
The idea behind the Naive approach is to check at every node of the main tree whether a subtree matches the given subtree.
Follow the steps below to solve the problem:
- Traverse the tree with root as root1 in preorder manner.
- For every visited node in the traversal, check if the subtree rooted at this node is identical to tree with root as root2.
- To check if the subtree is identical, traverse both trees simultaneously.
- If a visited node's value is not equal to the corresponding node in the other tree, return false. Otherwise, continue traversing until the whole subtree is verified.
Below is the implementation of above approach:
C++
// C++ Program to Check if a Binary Tree is subtree
// of another binary tree
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* left;
Node* right;
Node(int value) {
data = value;
left = nullptr;
right = nullptr;
}
};
// Utility function to check if two trees are identical
bool areIdentical(Node* root1, Node* root2) {
if (root1 == nullptr && root2 == nullptr)
return true;
if (root1 == nullptr || root2 == nullptr)
return false;
// Check if data and left/right subtrees are identical
return (root1->data == root2->data &&
areIdentical(root1->left, root2->left) &&
areIdentical(root1->right, root2->right));
}
// Function to check if root2 is a subtree of root1
bool isSubtree(Node* root1, Node* root2) {
if (root2 == nullptr)
return true;
if (root1 == nullptr)
return false;
// Check if the current node of root1 matches
// the root of root2
if (areIdentical(root1, root2))
return true;
// Recur for left and right subtrees of root1
return isSubtree(root1->left, root2)
|| isSubtree(root1->right, root2);
}
int main() {
// Construct Tree root1
// 26
// / \
// 10 3
// / \ \
// 4 6 3
// \
// 30
Node* root1 = new Node(26);
root1->right = new Node(3);
root1->right->right = new Node(3);
root1->left = new Node(10);
root1->left->left = new Node(4);
root1->left->left->right = new Node(30);
root1->left->right = new Node(6);
// Construct Tree root2
// 10
// / \
// 4 6
// \
// 30
Node* root2 = new Node(10);
root2->right = new Node(6);
root2->left = new Node(4);
root2->left->right = new Node(30);
if (isSubtree(root1, root2))
cout << "true";
else
cout << "false";
return 0;
}
// C Program to Check if a Binary Tree is
// subtree of another binary tree
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node* left;
struct Node* right;
};
// Utility function to check if two trees are identical
int areIdentical(struct Node* root1, struct Node* root2) {
if (root1 == NULL && root2 == NULL)
return 1;
if (root1 == NULL || root2 == NULL)
return 0;
// Check if data and left/right subtrees are identical
return (root1->data == root2->data &&
areIdentical(root1->left, root2->left) &&
areIdentical(root1->right, root2->right));
}
// Function to check if root2 is a subtree of root1
int isSubtree(struct Node* root1, struct Node* root2) {
if (root2 == NULL)
return 1;
if (root1 == NULL)
return 0;
// Check if the current node of root1 matches
// the root of root2
if (areIdentical(root1, root2))
return 1;
// Recur for left and right subtrees of root1
return isSubtree(root1->left, root2)
|| isSubtree(root1->right, root2);
}
struct Node* createNode(int value) {
struct Node* newNode =
(struct Node*)malloc(sizeof(struct Node));
newNode->data = value;
newNode->left = newNode->right = NULL;
return newNode;
}
int main() {
// Construct Tree root1
// 26
// / \
// 10 3
// / \ \
// 4 6 3
// \
// 30
struct Node* root1 = createNode(26);
root1->right = createNode(3);
root1->right->right = createNode(3);
root1->left = createNode(10);
root1->left->left = createNode(4);
root1->left->left->right = createNode(30);
root1->left->right = createNode(6);
// Construct Tree root2
// 10
// / \
// 4 6
// \
// 30
struct Node* root2 = createNode(10);
root2->right = createNode(6);
root2->left = createNode(4);
root2->left->right = createNode(30);
if (isSubtree(root1, root2))
printf("true");
else
printf("false");
return 0;
}
// Java Program to Check if a Binary Tree is
// subtree of another binary tree
class Node {
int data;
Node left;
Node right;
Node(int value) {
data = value;
left = null;
right = null;
}
}
class GfG {
// Utility function to check if two trees are identical
static boolean areIdentical(Node root1, Node root2) {
if (root1 == null && root2 == null)
return true;
if (root1 == null || root2 == null)
return false;
// Check if data and left/right subtrees are identical
return (root1.data == root2.data &&
areIdentical(root1.left, root2.left) &&
areIdentical(root1.right, root2.right));
}
// Function to check if root2 is a subtree of root1
static boolean isSubtree(Node root1, Node root2) {
if (root2 == null)
return true;
if (root1 == null)
return false;
// Check if the current node of root1 matches
// the root of root2
if (areIdentical(root1, root2))
return true;
// Recur for left and right subtrees of root1
return isSubtree(root1.left, root2)
|| isSubtree(root1.right, root2);
}
public static void main(String[] args) {
// Construct Tree root1
// 26
// / \
// 10 3
// / \ \
// 4 6 3
// \
// 30
Node root1 = new Node(26);
root1.right = new Node(3);
root1.right.right = new Node(3);
root1.left = new Node(10);
root1.left.left = new Node(4);
root1.left.left.right = new Node(30);
root1.left.right = new Node(6);
// Construct Tree root2
// 10
// / \
// 4 6
// \
// 30
Node root2 = new Node(10);
root2.right = new Node(6);
root2.left = new Node(4);
root2.left.right = new Node(30);
if (isSubtree(root1, root2))
System.out.println("true");
else
System.out.println("false");
}
}
# Python Program to Check if a Binary Tree is subtree
# of another binary tree
class Node:
def __init__(self, value):
self.data = value
self.left = None
self.right = None
# Utility function to check if two trees are identical
def areIdentical(root1, root2):
if root1 is None and root2 is None:
return True
if root1 is None or root2 is None:
return False
# Check if data and left/right subtrees are identical
return (root1.data == root2.data and
areIdentical(root1.left, root2.left) and
areIdentical(root1.right, root2.right))
# Function to check if root2 is a subtree of root1
def isSubtree(root1, root2):
if root2 is None:
return True
if root1 is None:
return False
# Check if the current node of root1 matches
# the root of root2
if areIdentical(root1, root2):
return True
# Recur for left and right subtrees of root1
return isSubtree(root1.left, root2) or \
isSubtree(root1.right, root2)
if __name__ == "__main__":
# Construct Tree root1
# 26
# / \
# 10 3
# / \ \
# 4 6 3
# \
# 30
root1 = Node(26)
root1.right = Node(3)
root1.right.right = Node(3)
root1.left = Node(10)
root1.left.left = Node(4)
root1.left.left.right = Node(30)
root1.left.right = Node(6)
# Construct Tree root2
# 10
# / \
# 4 6
# \
# 30
root2 = Node(10)
root2.right = Node(6)
root2.left = Node(4)
root2.left.right = Node(30)
if isSubtree(root1, root2):
print("true")
else:
print("false")
// C# Program to Check if a Binary Tree is
// subtree of another binary tree
using System;
class Node {
public int data;
public Node left;
public Node right;
public Node(int value) {
data = value;
left = null;
right = null;
}
}
class GfG {
// Utility function to check if two trees are identical
static bool AreIdentical(Node root1, Node root2) {
if (root1 == null && root2 == null)
return true;
if (root1 == null || root2 == null)
return false;
// Check if data and left/right subtrees are identical
return (root1.data == root2.data &&
AreIdentical(root1.left, root2.left) &&
AreIdentical(root1.right, root2.right));
}
// Function to check if root2 is a subtree of root1
static bool isSubtree(Node root1, Node root2) {
if (root2 == null)
return true;
if (root1 == null)
return false;
// Check if the current node of root1
// matches the root of root2
if (AreIdentical(root1, root2))
return true;
// Recur for left and right subtrees of root1
return isSubtree(root1.left, root2)
|| isSubtree(root1.right, root2);
}
static void Main() {
// Construct Tree root1
// 26
// / \
// 10 3
// / \ \
// 4 6 3
// \
// 30
Node root1 = new Node(26);
root1.right = new Node(3);
root1.right.right = new Node(3);
root1.left = new Node(10);
root1.left.left = new Node(4);
root1.left.left.right = new Node(30);
root1.left.right = new Node(6);
// Construct Tree root2
// 10
// / \
// 4 6
// \
// 30
Node root2 = new Node(10);
root2.right = new Node(6);
root2.left = new Node(4);
root2.left.right = new Node(30);
if (isSubtree(root1, root2))
Console.WriteLine("true");
else
Console.WriteLine("false");
}
}
// JavaScript Program to Check if a Binary
// Tree is subtree of another binary tree
class Node {
constructor(value) {
this.data = value;
this.left = null;
this.right = null;
}
}
// Utility function to check if two
// trees are identical
function areIdentical(root1, root2) {
if (root1 === null && root2 === null)
return true;
if (root1 === null || root2 === null)
return false;
// Check if data and left/right subtrees are identical
return (root1.data === root2.data &&
areIdentical(root1.left, root2.left) &&
areIdentical(root1.right, root2.right));
}
// Function to check if root2 is a subtree of root1
function isSubtree(root1, root2) {
if (root2 === null)
return true;
if (root1 === null)
return false;
// Check if the current node of root1
// matches the root of root2
if (areIdentical(root1, root2))
return true;
// Recur for left and right subtrees of root1
return isSubtree(root1.left, root2)
|| isSubtree(root1.right, root2);
}
// Construct Tree root1
// 26
// / \
// 10 3
// / \ \
// 4 6 3
// \
// 30
const root1 = new Node(26);
root1.right = new Node(3);
root1.right.right = new Node(3);
root1.left = new Node(10);
root1.left.left = new Node(4);
root1.left.left.right = new Node(30);
root1.left.right = new Node(6);
// Construct Tree root2
// 10
// / \
// 4 6
// \
// 30
const root2 = new Node(10);
root2.right = new Node(6);
root2.left = new Node(4);
root2.left.right = new Node(30);
if (isSubtree(root1, root2))
console.log("true");
else
console.log("false");
Time Complexity: O(n^2) where n is number of nodes of a Binary tree.
Auxiliary space: O(n) where n is number of nodes of a Binary tree.
Related articles: