Abstract
“If the tower is any taller than 320 ms, it may collapse,” Eiffel thinks out loud. Although understanding this counterfactual poses no trouble, the most successful interventionist semantics struggle to model it because the antecedent can come about in infinitely many ways. My aim is to provide a semantics that will make modeling such counterfactuals easy for philosophers, computer scientists, and cognitive scientists who work on causation and causal reasoning. I first propose three desiderata that will guide my theory: it should be general, yet conservative, yet useful. Next, I develop a formalization of events in the form of an algebra. I identify an event with all the ways in which it can be brought about and provide rules for determining the referent of an arbitrary event description. I apply this algebra to counterfactuals expressed using underdeterministic causal models-models that encode non-probabilistic causal indeterminacies. Specifically, I develop semaphore interventions, which represent how the target system may be modified from without in a coordinated fashion. This, in turn, allows me to bring about any event within a single model. Finally, I explain the advantages of this semantics over other interventionist competitors.
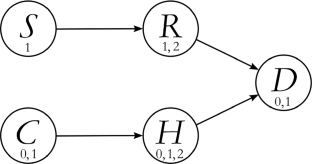
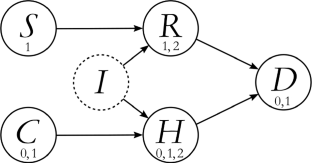
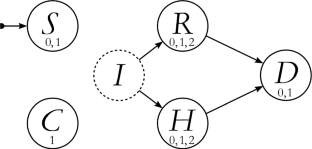
Similar content being viewed by others
Notes
Fine’s semantics also requires an additional set of situations that falsify a proposition. In the interventionist context, they aren’t relevant, and both Briggs’s and my theory do without them.
If \(\vec {Y}\) is a single variable, Y, I’ll abuse the notation and typically let \(\vec {x}[Y]\) denote Y’s value instead of the assignment over one value, e.g., \(\left\langle 1_C, 2_H, 0_R \right\rangle [H]=2\) instead of \(\left\langle 1_C, 2_H, 0_R \right\rangle [H]=\left\langle 2_H \right\rangle \). A projection onto an empty list of variables produces the empty assignment, \(\vec {x}[\emptyset ]=\left\langle \right\rangle \).
This requirement rules out expressions where, for example, you divide by 0.
Events are similar to teams (Barbero & Sandu, 2021) in that they are sets of assignments; however, unlike teams, events can include assignments that aren’t over the same variables.
E.g., the set of worlds where \(\lnot p\) holds is the complement of the set of worlds where p holds.
In both cases, construe the sets as sets of assignments over single variables. I.e., \((200, 300]_T = \left\{ \left\langle t \right\rangle :200 < t \le 300\right\} \).
For an extensive motivation, see (Wysocki, 2023b).
See footnote 9 for why I use the future tense.
In describing non-deterministic cases, I prefer to use the future tense, which makes it easier to think about the future as open. Once you know that Charybdis noticed the ship, you’re less likely to find not noticing the ship a genuine possibility. But the account doesn’t distinguish between counterfactuals and future conditionals.
Just read it as
 .
.Again, just read it as
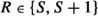 , where the set depends on S’s value.
, where the set depends on S’s value.Formally, I’ll construe structural equations as functions returning non-empty subsets of the variable’s range,
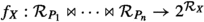 . Therefore, a model is essentially a system of constraints in the form
. Therefore, a model is essentially a system of constraints in the form 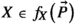 . An equation is deterministic if it returns a singleton for every input.
. An equation is deterministic if it returns a singleton for every input.Unfortunately, this convention won’t do justice to the entire model, as the diagram doesn’t show which values from different nodes belong to the same solution. I also won’t list the values of intervention vertices on the diagram.
I am referring here to deterministic causal models as used by, for example, Hitchcock (2001) and Weslake (2015), where both exogenous and endogenous variables are treated on par, having their values set by equations (just that exogenous equations are nullary). But you can treat exogenous variables differently. Like Halpern (2016:155) or Beckers and Vennekens (2017:11), you can set exogenous values with value vectors, called contexts, and ask what set of solutions is induced by some set of contexts. In such formalism, you can recover genuine notions of causal necessity and possibility, although not disjunctive interventions (because an intervention in this formalism always sets the target variable to a single value). As an aside, I’ll flag that I find it unbearably artificial to allow for underdeterminacy in exogenous variables (i.e., contexts) but not endogenous equations: whatever the motivation for introducing multiple contexts (e.g., to model either epistemic or genuinely metaphysical indeterminacy), it extends to endogenous variables.
For proofs, see (Wysocki, 2023b).
Although Günther (2017) also uses piecemeal models, his strategy is a little different. He proposes to evaluate a would-counterfactual with antecedent \(\varphi \) with a family of piecemeal models, each produced bringing about one of (what he calls) disjunctive situations of \(\varphi \): “\(A=a \vee B=b\) is satisfied if three possible situations are satisfied: (i) \(A=a \wedge B=b\), (ii) \(A=a \wedge B=\lnot b\), and (iii) \(A=\lnot a \wedge B=b\). We refer to (i)-(iii) as the disjunctive situations or possibilities of the formula \(A=a \vee B=b\).” Günther (2017):7. But like Briggs’s semantics, this strategy does not apply to infinite ranges.
Therefore, an underdeterministic semaphore intervention takes model \(\mathfrak {M}= \left\langle \vec {\mathcal {V}}, \vec {\mathcal {I}}, \mathcal {R} \mathcal {E} \right\rangle \) and a set of assignments \(J_i\) over variables \(\vec {X}\) (\(\vec {X}\subseteq \vec {\mathcal {V}}\), J cannot be further decomposed into a junction of juncts over non-overlapping variables) and returns a post-intervention model. In cases where \(\emptyset \ne J \ne \{\langle \rangle \}\) and the assignments from J aren’t all over the same single variable, the post-intervention model is given by
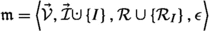 , where
, where 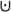 is exclusive union, I is a new intervention node, and \(\epsilon \) is the new set of equations. \(\epsilon \) contains the same structural equations as \(\mathcal {E}\) except for equations for I, which is given by (25), and for \(\vec {X}\), which are given by (26) and (27). If J only contains assignments over the same single variable X, X’s new equation is given by (28), and no intervention vertex is added to \(\mathfrak {m}\). If \(J=\{\langle \rangle \}\), \(\mathfrak {m}= \mathfrak {M}\). If \(J=\emptyset \), the operation cannot be performed.
is exclusive union, I is a new intervention node, and \(\epsilon \) is the new set of equations. \(\epsilon \) contains the same structural equations as \(\mathcal {E}\) except for equations for I, which is given by (25), and for \(\vec {X}\), which are given by (26) and (27). If J only contains assignments over the same single variable X, X’s new equation is given by (28), and no intervention vertex is added to \(\mathfrak {m}\). If \(J=\{\langle \rangle \}\), \(\mathfrak {m}= \mathfrak {M}\). If \(J=\emptyset \), the operation cannot be performed.Notice that I simplified how I encodes the values of B and C. An identical trick is possible with the previous model.
According to the notion of independence (21) applied to intervention vertices.
If the probabilities are 0, they sum to 0; if they are anything more than 0, their sum doesn’t exist (i.e., it’s infinite). In either case, they don’t sum to 1 and thus violate the probability axioms.
The theory has all the hallmarks of a causal decision theory. For instance, it’s possible to formulate an underdeterministic Newcomb’s case: I may or may not be predestined for hell; if I’m predestined for hell, and only then, will I sin and will I go to hell. Though I enjoy sinning, no time spent in hell is worth it. Going to hell and sinning are conditionally dependent per (21), yet I should sin, for doing so doesn’t cause my going to hell (Wysocki ms1).
This is an example of an underdeterministic parametric intervention, which I am about to discuss.
Also see Korb et al. (2004).
This would require using degenerate counterfactual distributions assigning 1 to the outcome of the structural equation and 0 to any other value from the range.
Of course, no mind or machine will store at once infinitely many solutions to a model. But the problem described applies, for instance, to the physically feasible task of checking whether some assignment is a solution to a model. (I’ll come back to this point soon.) Finite numerical representations will force a physically implemented probabilistic model to produce false negatives for infinitely many solutions.
Two variables may share no ancestors in every piecemeal model—and therefore be unconditionally independent—yet share an ancestor, an intervention node, in the model produced by the semaphore intervention.
The epistemic interpretation implies that an event is either causally necessary or causally impossible. “\(\varphi \) could have happened” is equivalent to the counterfactual “had everything been as it was, \(\varphi \) could have happened,”
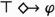 ; therefore, according to the epistemic interpretation, “\(\varphi \) could have happened” is equivalent to “it’s consistent with the speaker’s knowledge that \(\varphi \) would have happened.” This means that observing that \(\varphi \) happens (doesn’t happen) compels the speaker to think that \(\varphi \) was causally necessary (impossible). In short: the epistemic interpretation entails that statements of the form “the coin landed heads but could have landed tails” are infelicitous Moore’s sentences. In contrast, the underdeterministic treatment judges such sentences as felicitous.
; therefore, according to the epistemic interpretation, “\(\varphi \) could have happened” is equivalent to “it’s consistent with the speaker’s knowledge that \(\varphi \) would have happened.” This means that observing that \(\varphi \) happens (doesn’t happen) compels the speaker to think that \(\varphi \) was causally necessary (impossible). In short: the epistemic interpretation entails that statements of the form “the coin landed heads but could have landed tails” are infelicitous Moore’s sentences. In contrast, the underdeterministic treatment judges such sentences as felicitous.The rules also work if \(\vec {\sigma }\) is an assignment over \(\vec {\mathcal {V}}\) only.
I use \(\mathfrak {M}^{\top }\) for the set of all solutions, as elsewhere (Wysocki, 2023b) I use \(\mathfrak {M}^{\psi }\) for the set of all solutions that satisfy \(\psi \).
I.e., \(U_{\vec {X}}\) contains assignments over variables from \(\vec {X}\), though not every assignment needs to be over \(\vec {X}\). \(U_{\vec {X}}[\vec {P}]\) contains assignments from \(U_{\vec {X}}\) where the values for \(\vec {X}\backslash \vec {P}\) have been trimmed off from the assignments.
References
Andreas, H., & Günther, M. (2021). Difference-making causation. Journal of Philosophy, 118(12), 680–701.
Bell, J. L. (2016). Infinitary Logic. The Stanford Encyclopedia of Philosophy, Edward N. Zalta (Ed.). https://plato.stanford.edu/archives/win2016/entries/logic-infinitary/.
Barbero, F., & Sandu, G. (2021). Team semantics for interventionist counterfactuals: Observations vs. interventions. Journal of Philosophical Logic, 50(3), 471–521.
Beckers, S., & Vennekens, J. (2017). The transitivity and asymmetry of actual causation. Ergo, 4(1), 1–27.
Bennett, J. (2003). A philosophical guide to conditionals. Oxford: Oxford University Press.
Biswas, T. (1997). Decision-making under uncertainty. Cambridge: MIT Press.
Blanchard, T., & Schaffer, J. (2017). Cause without default. Beebee (pp. 175–214). Price, making a difference. Oxford: Hitchcock.
Briggs, R. A. (2012). Interventionist counterfactuals. Philosophical Studies, 160(1), 139–166.
Cohen, M., & Jaffray, J. (1983). Rational choice under complete ignorance. Econometrica, 48, 1281–1299.
Deœux, T. (2019). Decision-making with belief functions: A review. International Journal of Approximate Reasoning, 109, 87–110.
DeRose, K. (1999). Can it be that it would have been even though it might not have been? Philosophical Perspectives, 13, 385–413.
Eberhardt, F., & Scheines, R. (2006). Interventions and causal inference. Philosophy of Science, 74(5), 981–995.
Edgington, D. (2004). Counterfactuals and the benefit of hindsight. In Dowe & Noordhof (Eds.), Cause and chance: Causation in an indeterministic world. Routledge.
Ellis, B., Jackson, F., & Pargetter, R. (1977). An objection to possible-world semantics for counterfactual logics. Journal of Philosophical Logic, 6, 355–357.
Fenton-Glynn, L. (2017). A proposed probabilistic extension of the Halpern and pearl definition of ‘actual cause’. The British Journal for the Philosophy of Science, 68(4), 1061–1124.
Fine, K. (2012). Counterfactuals without possible worlds. The Journal of Philosophy, 109(3), 221–246.
Gallow, D. (ms.). Dependence, defaults, and needs.
Gallow, D. (2021). A model-invariant theory of causation. Philosophical Review, 130(1), 45–96.
Glymour, C., & Wimberly, F. (2007). Actual causes and thought experiments. In Silverstein O’Rourke (Ed.), Campbell (pp. 43–67). Cambridge: Causation and explanation.
Gerstenberg, T., & Tenenbaum, J. (2017). Intuitive theories. In M. Waldmannn (Ed.), Oxford handbook of causal reasoning (pp. 515–548). Oxford University Press.
Gopnik, A., Glymour, C., Sobel, D., Schulz, L., Kushnir, T., & Danks, D. (2004). A theory of causal learning in children: Causal maps and Bayes nets. Psychological Review, 111, 1–31.
Günther, M. (2017). Disjunctive antecedents for causal models. Proceedings of the 21st Amsterdam Colloquium.
Hájek, A. (2021). Counterfactual scepticism and antecedent-contextualism. Synthese, 199, 637–659.
Hall, N. (2004). Two concepts of causation. In Collins & Hall (Eds.), Counterfactuals and causation (pp. 225–276). Cambridge: MIT Press.
Hall, N. (2007). Structural equations and causation. Philosophical Studies, 132(1), 109–136.
Halpern, J. (2016). Actual causality. Cambridge, MA: MIT Press.
Halpern, J. (2000). Axiomatizing causal reasoning. Journal of Artificial Intelligence Research, 12, 317–337.
Halpern, J., & Pearl, J. (2005). Causes and explanations: A structural-model approach, part I: Causes. British Journal for the Philosophy of Science, 56(4), 843–87.
Halpern, J., & Hitchcock, C. (2015). Graded causation and defaults. British Journal for the Philosophy of Science, 66(2), 413–457.
Hiddleston, E. (2005). A causal theory of counterfactuals. Noûs, 39, 632–657.
Hitchcock, C. (2001). The intransitivity of causation revealed in equations and graphs. Journal of Philosophy, 98(6), 273–299.
Hitchcock, C. (2016). Conditioning, intervening, and decision. Synthese, 193(4), 1157–1176.
Huber, F. (2013). Structural equations and beyond. Review of Symbolic Logic, 6(4), 709–732.
Knight, F. (1921). Risk, uncertainty, and profit. Boston: Houghton Mifflin Company.
Korb, K., Hope, L., Nicholson, A., & Axnick, K. (2004). Varieties of causal intervention. In: Zhang, C. & Werner H. (Eds.), Pacific rim conference on artificial intelligence, New York, (pp. 322–31).
Lewis, D. (1973). Counterfactuals. Cambridge, MA: Harvard University Press.
Lewis, D. (1986). Events. In his Philosophical Papers (Vol. II, pp. 241–69). New York: Oxford University Press.
Meek, C., & Glymour, C. (1994). Conditioning and intervening. British Journal for the Philosophy of Science, 45(4), 1001–1021.
Menzies, Peter, & Price, Huw. (1993). Causation as a secondary quality. British Journal for the Philosophy of Science, 44(2), 187–203.
McDonald, J. (2023, Forthcoming). Essential structure for causal models. Australasian Journal of Philosophy.
Norton, J. (2021). Eternal inflation: When probabilities fail. Synthese, 198, 3853–3875.
Norton, John. (2003). Causation as folk science. Philosophers’. Imprint, 3, 1–22.
Pearl, J. (2009). Causality: Models, reasoning, and inference (2nd ed.). Cambridge: Cambridge University Press.
Pearl, J. (2011). The algorithmization of counterfactuals. Annals of Mathematics and Artificial Intelligence, 61(1), 29–39.
Quine, W. (1982). Methods of Logic. Cambridge, MA: Harvard University Press.
Rosella, G., & Sprenger, J. (2022). Causal modeling semantics for counterfactuals with disjunctive antecedents. Draft. https://philpapers.org/archive/ROSCMS-2.pdf.
Ross, L., & Woodward, J. (2022). Irreversible (one-hit) and reversible (sustaining) causation. Philosophy of Science, 89(5), 889–898.
Sartorio, C. (2006). Disjunctive causes. Journal of Philosophy, 103(10), 521–538.
Schaffer, J. (2004). Counterfactuals, causal independence and conceptual circularity. Analysis, 64(4), 299–308.
Stalnaker, R. (1968). A theory of conditionals. In Rescher (Ed.), Studies in logical theory (pp. 98–112). Oxford: Basil Blackwell.
Stalnaker, R. (1980). A defense of conditional excluded middle. In Harper, Stalnaker, & Pearce (Eds.), IFS. (Vol. 15). Dordrecht: Springer.
Twardy, C., & Korb, K. (2011). Actual causation by probabilistic active paths. Philosophy of Science, 78, 900–913.
Vandenburgh, J. (2022). Backtracking through interventions: An exogenous intervention model for counterfactual semantics. Mind & Language.
Verma, T., & Pearl. J. (1988). Causal Networks: Semantics and Expressiveness. Proceedings, 4th Workshop on Uncertainty in Artificial Intelligence, Minneapolis, MN 352-359.
Walters, L. (2009). Morgenbesser’s coin and counterfactuals with true components. Proceedings of the Aristotelian Society, 109(1), 365–379.
Weslake, B. (2015). A partial theory of actual causation. British Journal for the Philosophy of Science.
Williams, J. (2010). Defending conditional excluded middle. Noûs, 44(4), 650–668.
Woodward, J. (2003). Making things happen: A theory of causal explanation. Oxford: Oxford University Press.
Woodward, J. (2016). The problem of variable choice. Synthese, 193, 1047–1072.
Woodward, J. (2021). Causation with a human face: Normative theory and descriptive psychology. Oxford: Oxford University Press.
Wysocki, T. (2023a). Conjoined cases. Synthese, 201, 197.
Wysocki, T. (2023b). The Underdeterministic Framework. The British Journal for the Philosophy of Science. Forthcoming. 10.1086/724450
Wysocki, T. (ms1). Causal decision theory for the probabilistically blinded.
Wysocki, T. (ms2). Underdeterministic causation: a proof of concept.
Acknowledgements
This paper benefited greatly from the suggestions from the two reviewers, who seriously engaged with the paper and helped me clarify its contribution much better; from Ray Briggs and Jonathan Vandenburgh, who were my APA commentators and gave me both good feedback and encouragement; from Jim Woodward, Dmitri Gallow, Clark Glymour, and Colin Allen, who helped me shape this theory when it was still a thesis chapter; and from Jason Kay and Stephen Mackereth.
Funding
Funding was provided by Office for Science and Technology of the Embassy of France in the United States (Chateaubriand Fellowship 2022), Japan Society for the Promotion of Science London (Grant No. PE22039), and Deutsche Forschungsgemeinschaft (Reinhart Koselleck project WA 621/25-1).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
None declared.
Appendix
Appendix
1.1 The syntax and semantics of model statements
Here, I present the syntax and semantics of event names and model statements—the statements that can be true or false in a model—in one place.
First, the grammar:
production rule | ||
brick sentence | \(B \rightarrow \!\) | an expression over some variables from \(\vec {\mathcal {V}}\); |
the exact syntax depends on the ranges | ||
event name | \(E \rightarrow \!\) | B,\((\lnot E)\), \((E \wedge E)\), \((E \vee E)\), \((E \rightarrow E)\), \((E \equiv E)\), |
modal sentence | \(M \rightarrow \!\) | \(\mathop {\Box }E\), \(\mathop {\Diamond }E\), |
counterfactual | \(C \rightarrow \!\) |
|
model statement | \(S \rightarrow \!\) | (C), \((\lnot S)\), \((S \wedge S)\), \((S \vee S)\). |
In all cases used throughout, brick sentences were arithmetic equations or inequalities. The grammar allows for model statements like 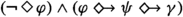 , but not for \(\mathop {\Box }\mathop {\Diamond }\varphi \) or
, but not for \(\mathop {\Box }\mathop {\Diamond }\varphi \) or 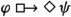 .
.
Let \(\mathfrak {M}\) be the (pre-intervention) model of evaluation, \(\mathfrak {M}^{\top }\) be the set of solutions to \(\mathfrak {M}\), \(\psi \) be a name over \(\vec {X}\) (\(\vec {X}\subseteq \vec {\mathcal {V}}\)), \(\varphi \) be any name of a consistent event (i.e., \(\llbracket \varphi \rrbracket \ne \emptyset \)) over some subset of \(\vec {\mathcal {V}}\), \(\vec {\sigma }\) be any assignment over all its nodes, 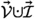 ,Footnote 29 and \(S_1\), \(S_2\) be any model statements.Footnote 30 Below is the full semantics; although it doesn’t need to be expressed in terms of the event algebra, it can, and I provide the alternative rules too:
,Footnote 29 and \(S_1\), \(S_2\) be any model statements.Footnote 30 Below is the full semantics; although it doesn’t need to be expressed in terms of the event algebra, it can, and I provide the alternative rules too:
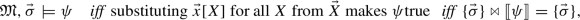
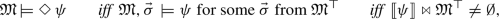
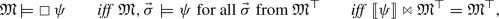
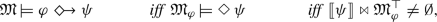

1.2 An event has at most one canonical form
Theorem
A non-empty set of assignments over at least one variable has a single canonical form, which is the junction of the maximum number of assignment sets (juncts) over non-overlapping variables:
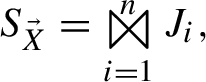
where: \(S_{\vec {X}}\) is over variables \(\vec {X}\), \(\vec {X}\ne \emptyset \), assignments from \(J_i\) don’t share variables with assignments from \(J_j\) (\(i\ne j\)), and \(J_i \ne \{\langle \rangle \}\).
Proof
The proof will be by induction on the maximum number of juncts the event decomposes into. First, notice that if a set of assignments is a junction of other sets of assignments, then the projection of the former onto some variables is a junction of the projections of the latter:
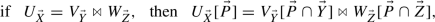
where \(\vec {X}=\vec {Y}\cup \vec {Z}\), \(\vec {P}\subseteq \vec {X}\), and \(U_{\vec {X}}[\vec {P}]\) is a projection of \(U_{\vec {X}}\) onto \(\vec {P}\) (read \(V_{\vec {Y}}[\vec {P}\cap \vec {Y}]\) and \(W_{\vec {Z}}[\vec {P}\cap \vec {Z}]\) analogously).Footnote 31 This property follows from (1), the definition of junction, because if an assignment is a spatial concatenation of two other assignments, then a projection of the former is a spatial concatenation of the corresponding projections of the latter.
Now, for the inductive part of the proof.
Base step The event denoted by any sentence over one variable is already in the canonical form. (The only non-empty set of assignments over no variables is \(\llbracket \top \rrbracket = \{\langle \rangle \}\); as a convention, assume that this is its canonical form.)
Inductive step Assume property (40) holds for sentences over fewer than k variables. Take \(S_{\vec {X}}\), a set of assignments over k variables. If \(S_{\vec {X}}\) doesn’t decompose any further, it trivially satisfies the property, as the set is already in the canonical form.
Otherwise, decompose \(S_{\vec {X}}\) as
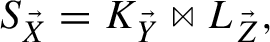
where 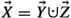 , \(\vec {Y}\ne \emptyset \ne \vec {Z}\), and \(L_{\vec {Z}}\) doesn’t decompose any further. As \(K_{\vec {Y}}\) is now over fewer than k variables, in virtue of the inductive assumption,
, \(\vec {Y}\ne \emptyset \ne \vec {Z}\), and \(L_{\vec {Z}}\) doesn’t decompose any further. As \(K_{\vec {Y}}\) is now over fewer than k variables, in virtue of the inductive assumption, 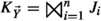 for some n and conjuncts \(\left\{ J_i\right\} _{i=1}^n\). Therefore, the canonical form for the target set is:
for some n and conjuncts \(\left\{ J_i\right\} _{i=1}^n\). Therefore, the canonical form for the target set is:
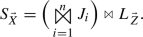
What’s left is to prove that this decomposition is unique. Decompose \(S_{\vec {X}}\) into any two juncts:
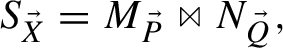
where 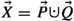 , and \(\vec {P}\ne \emptyset \ne \vec {Q}\). Either \(\vec {Z}\subseteq \vec {Q}\) or \(\vec {Z}\subseteq \vec {P}\), because otherwise, per (41),\(L_{\vec {Z}}\) could be decomposed further into two juncts: one over some variables from \(\vec {Q}\) and the other over some variables from \(\vec {P}\). For focus, assume \(\vec {Z}\subseteq \vec {Q}\). This means that
, and \(\vec {P}\ne \emptyset \ne \vec {Q}\). Either \(\vec {Z}\subseteq \vec {Q}\) or \(\vec {Z}\subseteq \vec {P}\), because otherwise, per (41),\(L_{\vec {Z}}\) could be decomposed further into two juncts: one over some variables from \(\vec {Q}\) and the other over some variables from \(\vec {P}\). For focus, assume \(\vec {Z}\subseteq \vec {Q}\). This means that 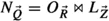 , where \(\vec {R}= \vec {Q}\backslash \vec {Z}\). Therefore,
, where \(\vec {R}= \vec {Q}\backslash \vec {Z}\). Therefore,
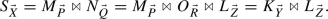
In virtue of the inductive assumption, 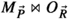 has a unique canonical form, and it’s the same as the one for \(K_{\vec {Y}}\), because
has a unique canonical form, and it’s the same as the one for \(K_{\vec {Y}}\), because 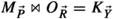 . That in turn means that (43) still gives the canonical form of \(S_{\vec {X}}\). Therefore, \(S_{\vec {X}}\) has a unique canonical form. This completes the inductive proof. \(\square \)
. That in turn means that (43) still gives the canonical form of \(S_{\vec {X}}\). Therefore, \(S_{\vec {X}}\) has a unique canonical form. This completes the inductive proof. \(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wysocki, T. An event algebra for causal counterfactuals. Philos Stud 180, 3533–3565 (2023). https://doi.org/10.1007/s11098-023-02015-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11098-023-02015-4


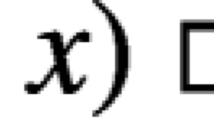

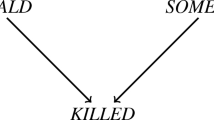
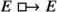 ,
, 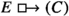 ,
, 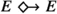 ,
, 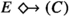 ,
,