I'm working with the Welder proof assistant. Basically, this system uses basic inference rules to modify the goal one wants to proof. At a latter step, the modified goals are passed to a SMT solver to see if it can prove them. I have already written automatic induction tactics that generate by themselves the induction hypothesis.
Now I want to write a procedure that will allow me to solve automatically the following problem:
Proof basic field theory statements using the axioms of group and already proved lemmas.
Could you describe successful approaches to solve this problem?
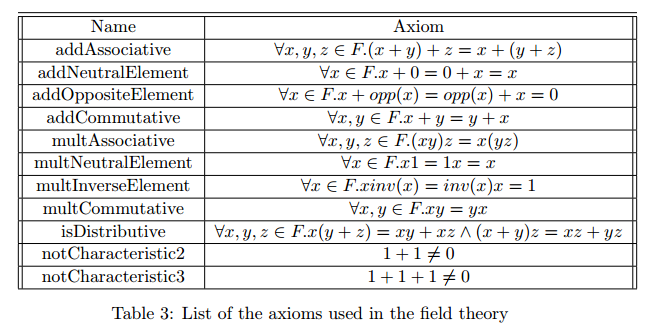
Here I leave you the kind of axioms that I want to use:
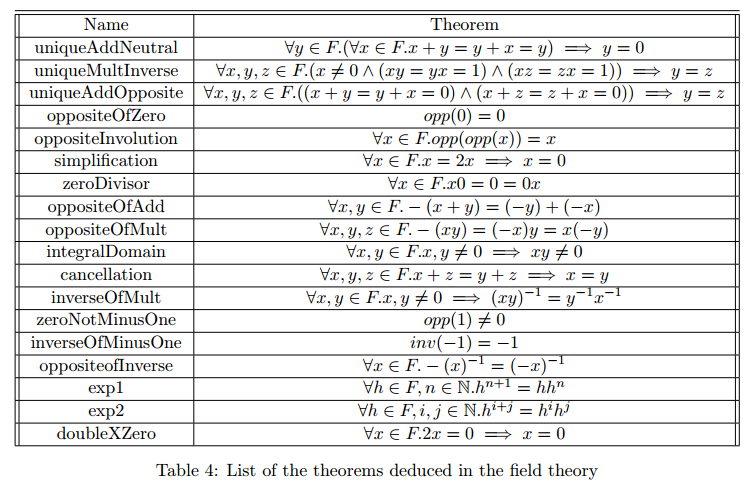
And here you have the kind of goals I would like to proof automatically:
The idea is that the procedure is given the theorem, a list of lemmas (axioms of other proved theorems) and is able to deduce by itselfdeduce by itself the goal.