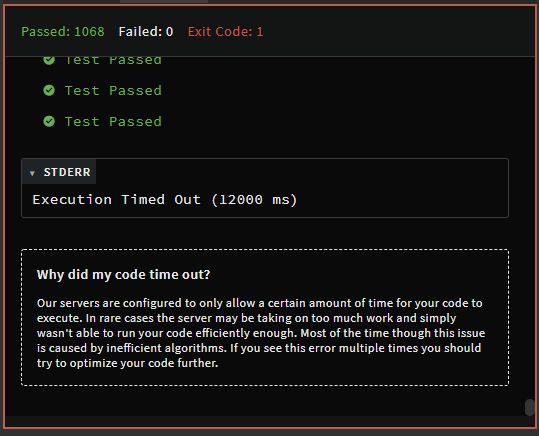
I am continuously timing out on the mentioned kata:

Task You will be given an array of random integers and a number n. You have to extract n smallest integers out of it preserving the original order.

##Examples

performant_smallest([1, 2, 3, 4, 5], 3) == [1, 2, 3] performant_smallest([5, 4, 3, 2, 1], 3) == [3, 2, 1] performant_smallest([1, 2, 3, 4, 1], 3) == [1, 2, 1] performant_smallest([1, 2, 3, -4, 0], 3) == [1, -4, 0] performant_smallest([2, 1, 3, 2, 3], 3) == [2, 1, 2]

##Notes

• The number n will always be smaller then the array length
• There will be duplicates in the array, and they have to be returned in the order of their each separate appearence
  Your solution has to be at least as fast as reference, passing the tests in 12000+ ms
• If you didn't pass a small amount of tests, try submitting again. Otherwise, your solution is not efficient enough.

##Test suite

Tests: 1500 Array size: 4500 Numbers range: [-100..100] Number of elements to return: 50-100% of the array

Note: you can't use Python 2

I wrote several different functions for this:

from heapq import *
from collections import Counter as count
from copy import copy

def heap_pop(lst, n):
    heap, res, i = copy(lst), [0]*n, 0
    heapify(heap)
    c = count(heappop(heap) for _ in range(n))
    for itm in lst:
        if c.get(itm, 0) > 0:
            res[i] = itm
            i += 1
            c[itm] -= 1
        if i == n: break
    return res

def sorting(lst, n):
    res, i = [0]*n, 0
    c = count(sorted(lst)[:n])
    for itm in lst:
        if c.get(itm, 0) > 0:
            res[i] = itm
            i += 1
            c[itm] -= 1
        if i == n: break
    return res

def n_smallest(lst, n):
    heap, res, i = copy(lst), [0]*n, 0
    heapify(heap)
    c = count(nsmallest(n, heap))
    for itm in lst:
        if c.get(itm, 0) > 0:
            res[i] = itm
            i += 1
            c[itm] -= 1
        if i == n: break
    return res

def counter_sort(lst, n):
    c = count(lst)
    d, x, res, sm = sorted(c), {}, [0]*n, 0
    for k in d:
        z = min(c[k], n-sm)
        x[k] = z
        sm += z
        if sm == n: break
    sm = 0
    for itm in lst:
        if x.get(itm, 0) > 0:
            res[sm] = itm
            sm += 1
            x[itm] -= 1
        if sm == n:     break
    return res

def cs2(lst, n):
    c = count(lst)
    d, x, res, sm = sorted(c), {}, [0]*n, 0
    for k in d:
        z = min(c[k], n-sm)
        x[k] = z
        sm += z
        if sm == n:     break
    sm = 0
    for itm in (itm for itm in lst if itm in x):
        if x.get(itm, 0) > 0:
            res[sm] = itm
            sm += 1
            x[itm] -= 1
        if sm == n: break
    return res

def csx(lst, n):
    c, sm = {i: 0 for i in range(-100, 101)}, 0
    for itm in lst:     c[itm] += 1
    d, x, res, sm = sorted(c), {}, [0]*n, 0
    for k in d:
        z = min(c[k], n-sm)
        x[k] = z
        sm += z
        if sm == n: break
    sm = 0
    for itm in (itm for itm in lst if itm in x):
        if x.get(itm, 0) > 0:
            res[sm] = itm
            sm += 1
            x[itm] -= 1
        if sm == n: break
    return res

I benchmarked all of them (lst is 4500 random numbers in [-100, 100], and n in [2250, 4500] with 10000 iterations) to simulate the actual data set. I'm very surprised that counter sort did not work considering that it is linear time and there were only two O(2) iterations in it.
counter_sort() was the clear best performer, but it only gets to 1068 of the test cases before failing.